Задача оптимизации норм обслуживания и норм численности рабочих при многостаночном обслуживании заключается в определении оптимального соотношения между количеством единиц оборудования и числом обслуживающих это оборудование рабочих. Предположим, что на предприятии имеется определенное количество технических устройств (металлорежущих станков, прессов, ЭВМ, тракторов и т.п.).
Как определить, сколько механиков потребуется для обслуживания этой техники? Ведь если механиков будет мало, то предприятие понесет убытки из-за простоя машин в ожидании обслуживания, а если много, то может существенно возрасти себестоимость изготовленных изделий (выполнения работ) на данном оборудовании в связи с увеличением затрат на содержание обслуживающего персонала.
Рассматриваемая задача решается с использованием методов теории массового обслуживания (ТМО).
Прежде всего, следует определить интенсивность потока отказов 
имеющегося оборудования (поток отказов сложных технических устройств обычно пуассоновский). Закон распределения времени обслуживания и его характеристики можно найти, проведя регистрацию длительности интервалов обслуживания.
Пусть оказалось, что по группе станочного оборудования интенсивность отказов =0,57, а интенсивность ремонта 
=0,8 (закон распределения времени ремонта - экспоненциальный). Так как????, то для осуществления ремонтных работ достаточно иметь одного механика, однако при этом возможны случаи простоя станков в ожидании обслуживания (очередь).
Можно определить вероятность того, что в очереди будет находиться l станков и вероятность отсутствия очереди P0.
P0=1-Ã: Рl =Ãl(1-Ã)при l = 1,2,3,..., где 
Вероятность отсутствия очереди для нашего примера равна:
При достаточно большом времени работы системы Р0 есть среднее значение того времени, когда очереди в системе нет. В данном случае очередь отсутствует примерно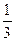 
времени работы. Подставляя различные значения l в формулу для Рl, получим, что среднее время существования очереди из одного станка равно 0,228 общего времени, из двух 0,15 и т.д.
Среднее время ожидания в очереди равно:
Среднее время ожидания в системе включает в себя время ожидания в очереди и время обслуживания равно:
;
;
Если ремонтом занимается n механиков (многоканальная система обслуживания), среднее время ожидания в очереди подсчитывается по формуле:
Для многоканальной системы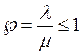 
. Величина Р0 обычно берется из графиков. Для построения этих графиков можно пользоваться таблицей Р0 для разных 
и n (табл. 1).
Таблица 1
| Ã | n | ||||||
| ... | |||||||
| 0,333 | 0,367 | 0,367 | 0,367 | 0,367 | 0,367 | 0,368 | |
| 0,111 | 0,130 | 0,134 | 0,135 | 0,135 | 0,135 | ||
| 0,037 | 0,046 | 0,049 | 0,049 | 0,050 | |||
| 0,013 | 0,016 | 0,017 | 0,018 |
Пусть оказалось, что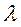 
=1,6; 
=0,9;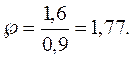 
Рассчитаем время ожидания в очереди и в системе при числе механиков n=2,3 и 4.
n=2; 
n=3; 
n=4;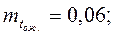 
За время T в систему обслуживания (группа механиков) поступает 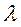Т заявок на ремонт. Общее время простоя станов в ожидании начала обслуживания и ремонте составляет 
единиц времени. Если потери от простоя станков, вызванные их пребыванием на обслуживании (уменьшается производительность за 1 час эксплуатационного времени), составляет 1 руб. В единицу времени, а стоимость содержания одного механика составляет 3 руб. в единицу времени, то затраты на содержание механиков и покрытие потерь от простоя станков будут характеризоваться следующими цифрами:
Таблица 2.
| Число механиков | Потери от простоя станков | Стоимость содержания механиков | Сумма затрат |
| 5,11 х 1,6 Т = 8,15 Т | 6 Т | 14,15 Т | |
| 1,42 х 1,6 Т = 2,28 Т | 9 Т | 11,28 Т | |
| 1,17 х 1,6 Т = 1,87 Т | 12 Т | 13,37 Т |
Сопоставляя эти цифры, мы видим, что наиболее экономично для обслуживания имеющейся техники иметь трех механиков.
Следует иметь ввиду, что в общем случае рассматриваемая система массового обслуживания является замкнутой, поскольку в ней поток поступающих заявок ограничен, а его интенсивность зависит от состояния самой системы, т.е. если на предприятии имеется К станков, то в системе обслуживания одновременно не может находиться больше К заявок.
При расчете оптимальных норм обслуживания для основных рабочих (например, в случае произвольного потока заявок на обслуживание) можно использовать имитационное моделирование на ЭВМ.
