Рассмотрим производственную систему - инструментальный склад, обслуживающий несколько цехов.
Руководитель предприятия, субъективно оценивая ситуацию, считает, что для обслуживания склада вполне достаточно одного кладовщика. Как получить научное обоснование такого решения?
Ситуации, подобные описанным, возникают в системах, называемых системами массового обслуживания (СМО).
Основываясь на предыдущем опыте, сделаем предположение о том, что поток требований пуассоновский. Для нахождения интенсивности потока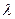 
будем регистрировать число пришедших на склад рабочих за каждые 15 минут на протяжении всего рабочего дня. В течение 5 рабочих дней сделано 140 наблюдений общей продолжительностью Т = 15 х 140 =2100 мин. При этом промежутков, когда на склад никто не приходил или приходил только один рабочий - не наблюдалось; двое рабочих приходили 1 раз; трое - 3 раза и т.д. Подсчитаем наблюденные частоты прихода разного количества рабочих, выразив их для удобства записи в процентах. Частота прихода двух рабочих, таким образом, оказывается раной 
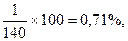трех - 2,14%, четырех - 5,72% и т.д. Полученные данные сводятся в таблицу (табл.1), где в первом столбце помещено наблюдаемое число m приходящих за 15 мин., во втором - общее число наблюдавшихся таких приходов, в третьем - вычисленная наблюденная частота.
Сумма цифр второго столбца равна общему числу наблюдений, т.е. 140. Из-за ошибок от округления при вычислении частот сумма цифр третьего столбца получилась равной 99,87%, а не 100%.
Чтобы найти среднее число приходов 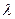в единицу времени, определим полное число приходов М как сумму попарных произведений цифр, стоящих в одинаковых строках первого и второго столбцов.
М = 2 х 1 + 3 х 3 + 4 х 8 +... + 19 х 1 = 1201
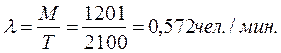
Проверим теперь, насколько допустима гипотеза о пуассоновском распределении потока. Для этого вычислим теоретическую частоту событий, равную вероятности поступления m требований (приходов) в данном интервале времени определяется по формуле (1). Поскольку период одного наблюдения t = 15 мин., то 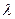Т = 15 х 0,572 = 8,58. По таблицам определяем е-8,58 = 0,000188 и m! Числа 8,58m находим для разных m = 0,1,2... 19 с помощью таблиц логарифмов. Произведя вычисления и умножив найденные значения теоретических частот на 100, получим четвертый столбец табл.1.
Таблица 1
| Число приходов за 15 мин. | Наблюдаемое число приходов за 140 наблюдений | Наблюдаемая частота приходов, % | Теоретическая частота приходов, % |
| 0,02 | |||
| 0,16 | |||
| 0,71 | 0,69 | ||
| 2,14 | 1,98 | ||
| 5,72 | 4,25 | ||
| 7,14 | 7,28 | ||
| 12,15 | 12,8 | ||
| 12,85 | 13,62 | ||
| 12,15 | 13,1 | ||
| 12,85 | 11,2 | ||
| 7,85 | 8,73 | ||
| 6,32 | 6,23 | ||
| 4,28 | 4,12 | ||
| 2,86 | 2,54 | ||
| 1,43 | 1,44 | ||
| 0,71 | 0,78 | ||
| 0,29 | |||
| 0,18 | |||
| 0,71 | 0,09 | ||
| Сумма | 99,87 | 99,5 |
Проверку согласованности теоретического и статистического распределений осуществим по критерию «Хи-квадрат» на основании анализа расхождений между теоретическими вероятностями Рi и наблюденными частотами Рik. Мера расхождения обычно обозначается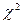 
. В данном случае получим:
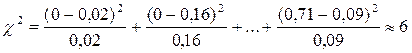
Входами в таблицах являются значения вероятности Р и число степени свободы r. Пользуясь таблицей, можно для каждого значения 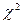и числа степеней свободы r найти вероятность того, что величина, распределенная по закону 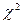, превзойдет это значение. Если вероятность Р сравнительно велика, можно признать расхождения между теоретическим и статистическим распределениями несущественными и отнести их за счет случайных причин.
Число степеней свободы равно числу разрядов минус число независимых условий («связей»), наложенных на частоты Рik.
В нашем примере таких независимых условий два, причем одним является требование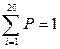 
, т.е. r =18. Для 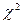=6 и r =18 вероятность Р будет больше 0,99 и, таким образом, гипотезу о пуассоновском распределении потока заявок можно считать не противоречащей опытным данным.
Далее, проведя регистрацию длительности интервалов обслуживания - экспоненциальный с интенсивностью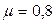 
и mtоб=1,25 мин. Так как оказалось, что 
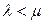, один кладовщик справиться с обслуживанием, однако будут иметь место случаи ожидания рабочими обслуживания (очередь), а кладовщики посетителей. Вероятность отсутствия очереди равна:
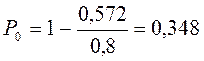
Сопоставив потери от простоя станков со стоимостью содержания 1,2,... кладовщиков, можно найти оптимальную численность кладовщиков (по аналогии с расчетом численности механиков).
Выбор оптимального варианта структуры управления.1
Проанализируем процесс функционирования одного из структурных подразделений предприятия (объединения), например, отдела материально-технического снабжения. Допустим, что в отделе работает n штатных сотрудников, которые занимаются обслуживанием требований (заявок на поставку сырья, комплектующих изделий и т.д.), поступающие в отдел. Интенсивность поступления заявок на обслуживание и время обслуживания одной заявки являются случайными величинами. Для удобства анализа примем следующую дисциплину обслуживания: требование, поступившее в отдел, когда все работники заняты обслуживанием других, ранее поступивших заявок, теряется. В реальных условиях в подобных случаях к обслуживанию заявки (в зависимости от ее важности) привлекаются работники других служб предприятия (при необходимости может быть определено и число ожидающих заявок).
Процесс функционирования рассмотренного структурного подразделения предприятия может быть описан в терминах систем массового обслуживания с n идентичными приборами - каналами обслуживания и числом мест для ожидания, равным нулю.
Как показали приведенные на ряде заводов машиностроительной промышленности исследования, законы распределения промежутка времени обслуживания одной заявки в большинстве случаев могут быть приняты экспоненциальными (поток заявок пуассоновский). Причем, в зависимости от характера производства и размеров предприятия характеристики закона распределения изменяются в широких пределах.
Обозначим через 
интенсивность потока заявок. Поступившая в отдел заявка направляется для обслуживания к любому свободному сотруднику. Время ее обслуживания имеет функцию распределения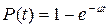 
и не зависит от сотрудника, к которому она направлена.
Используя модифицированные обозначения Кендалла, описанную систему можно классифицировать как
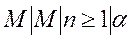
где М - экспоненциальное распределение времени поступления заявок;
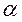- система с потерями.
Покажем на условных числовых параметрах возможность использования предложенной модели для анализа процесса функционирования звеньев аппарата управления и выбора оптимального, относительно принятого критерия, варианта структуры управления.
Пример 1. Пусть имеем предприятия А и В. На первом предприятии в отделе материально-технического снабжения работает 3 человека (n1 = 3), на втором - 2 человека (n2 = 2); интенсивность потока требований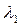 
= 3 (заявки в день), 
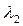= 2 (заявки в день); среднее время обслуживания одной заявки mtоб = 2 дня (
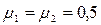). Определим вероятность того, что поступившее требование получит отказ в обслуживании. Приведенная плотность потока заявок 
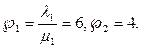По формуле Эрланга для установившегося режима находим вероятность отказа в обслуживании (критерий качества функционирования системы).
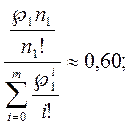
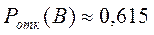
Пример 2. Посмотрим, как изменится вероятность отказа в обслуживании заявки, если отделы снабжения обоих предприятий объединить в один отдел (при прежних условиях поступления и обслуживания заявок).
