Невозможны такие процессы, единственным конечным результатом которых явилось бы отнятие от некоторого тела определенного количества тепла и превращение этого тепла полностью в работу;
3. энтропия изолированной системы не может убывать при любых происходящих в ней процессах:
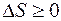, (8.6)
Где знак равенства относится к обратимым процессам, а знак больше – к необратимым процессам.
Энтропию можно связать со степенью упорядоченности системы. При необратимом процессе система переходит из менее вероятного упорядоченного состояния в более вероятное, неупорядоченное. Увеличение энтропии соответствует увеличению беспорядка системы. Энтропия – это мера беспорядка.
Формула Больцмана связывает энтропию S и термодинамическую вероятность W:
, (8.7)
где k – постоянная Больцмана. Термодинамическая вероятность (статистический вес)тела или системы W равна числу всевозможных микрораспределений частиц по координатам и скоростям, соответствующих данному термодинамическому состоянию (макросостоянию). Формула Больцмана позволяет дать статистическое истолкование второго закона термодинамики: термодинамическая вероятность состояния изолированной системы при всех происходящих в ней процессах не может убывать.
При нарушении равновесия система стремится вернуться в равновесное состояние. Этот процесс сопровождается возрастанием энтропии и, следовательно, необратим. Нарушение равновесия сопровождается возникновением потоков либо молекул, либо тепла, либо электрического заряда и т. п. В связи с этим соответствующие процессы называются явлениями переноса. Из сказанного выше вытекает, что явления переноса представляют собой необратимые процессы. Примерами таких явлений являются диффузия, вязкость, теплопроводность.
Среднее число соударений, испытываемых молекулой газа за 1 с:
, (8.8)
где d – эффективный диаметр молекулы; n – концентрация молекул; vср – средняя арифметическая скорость молекул.
Средняя длина свободного пробега молекул газа:
. (8.9)
Коэффициенты диффузии 
, вязкости 
и теплопроводности 
газов:
, 
, 
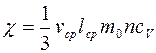, (8.10)
где 
- масса молекулы воздуха, 
- удельная теплоемкость воздуха при постоянном объеме.
Вопросы для самоподготовки
1. Дайте определение кругового процесса, прямого и обратного цикла.
2. Объясните, как работает тепловая машина. Что является рабочим телом в тепловой машине?
3. Какой процесс называют обратимым, а какой - необратимым? Приведите примеры таких процессов.
4. Дайте определение энтропии. Что происходит с энтропией изолированной системы при обратимом и необратимом процессах?
5. Какие процессы включает в себя цикл Карно?
6. В чем различие прямого и обратного циклов Карно?
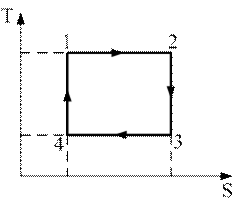
7. На рисунке 8.2. изображен цикл Карно в координатах (T,S), где S-энтропия. Назовите процессы, происходящие на каждом этапе.
|
8. Чему равен коэффициент полезного действия (КПД) тепловой машины, идеальной тепловой машины Карно?
9. В двигателе внутреннего сгорания температура образующихся при сгорании газов и зимой и летом примерно одинакова. Температура холодильника зимой ниже, чем летом. Это должно увеличивать КПД зимой (в соответствии с формулой Карно), однако зимой расход топлива больше, чем летом. Объясните почему.
10. Как работает холодильная машина? Чему равен холодильный коэффициент?
11. Меняет ли температуру воздуха в комнате работающий бытовой холодильник?
12. Изменится ли температура воздуха в комнате, если оставить открытой дверцу работающего холодильника?
13. Покажите эквивалентность различных формулировок второго начала термодинамики.
14. Запрещает ли второе начало термодинамики переход тепла от тела менее нагретого к телу более нагретому?
15. Дайте статистическое истолкование второго закона термодинамики.
16. Какие процессы называются явлениями переноса?
17. Какие явления переноса имеют место при наличии градиента концентрации, температуры, скорости слоев жидкости или газа?
Примеры решения задач
8.1. Идеальный газ совершает цикл, состоящий из изотермы, изобары и адиабаты, причем при изобарном процессе температура идеального газа увеличивается в n=2,5 раза. Определить к. п. д. данного цикла.
Дано: Найти:
Т2=2,5 Т1, .
Решение:
В условии задачи не оговорена последовательность процессов, но поскольку изобарный процесс, по условию, - процесс нагревания, следовательно, и расширения, то прямая, соответствующая графику этого процесса в координатах p, V, должна лежать выше кривых, изображающих изотермический и адиабатный процессы. После изобарного расширения 1-2 (рисунок 8.3) газ должен адиабатно расширяться (кривая 2-3) до тех пор, пока температура его не будет равна начальной температуре Т1, а затем изотермическим сжатием (кривая 3-1) газ можно вернуть в исходное состояние.
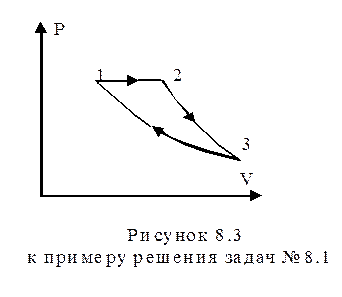
При последовательности процессов, изображенной на рисунке 8.3, газ получает теплоту только в процессе 1-2, поэтому Q1=Q12, и отдает теплоту в процессе 3-1 (
= 
). Процесс 2-3 происходит без теплообмена. Тогда к. п. д. цикла, согласно определению (8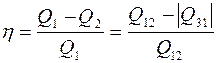.1):
. (1)
Количество теплоты, получаемое рабочим телом при изобарном процессе (7.16):
, (2)
где 
- молярная теплоемкость при постоянном давлении. Количество теплоты, отдаваемое рабочим телом при изотермическом сжатии (7.18):
. (3)
Для процесса 3-1 количество теплоты 
пропорционально 
. Поскольку V1<V3, логарифм будет отрицательным, поэтому в выражении для стоит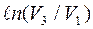 
.
Объемы газа и их отношения неизвестны, однако состояния 1 и 2 лежат на одной изобаре и
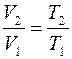. (4)
Состояния 2 и 3 лежат на одной адиабате, из уравнения Пуассона:
. (5)
Учитывая, что 
, и извлекая корень степени 
, можно получить:
. (6)
Перемножая почленно равенства (4) и (6), получим:
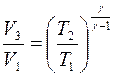. (7)
Тогда
. (8)
Если 
выразить через формулу (7.5), то выражение (8) примет вид:
. (9)
Если подставить (2) и (9) в (1), то можно получить выражение для к. п. д. данного цикла:
.
Ответ: 
.
2. Абсолютную температуру одного моля углекислого газа увеличили в n=2 раза сначала изобарно, а потом изохорно. Найти изменение энтропии в ходе указанных процессов. Газ считать идеальным.
Дано: Найти:
T2=2T1, 
,
, 
.
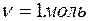1) p=const,
2) V=const.
Решение:
Приращение энтропии можно найти по формуле (8.5):
. (1)
При изобарном нагревании газ получает количество теплоты 
(7.16):
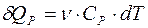, (2)
где CP =(i+2)R/2. Углекислый газ – газ трехатомный (i=6). Подставляя (2) в (1) и учитывая постоянство CP, можно получить:
. (3)
При изохорном нагревании газ получает количество теплоты (7.17):
, (4)
где CV =iR/2. Углекислый газ – газ трехатомный (i=6). Подставляя (4) в (1) и учитывая постоянство CV,можно получить:
.
Ответ: 
, 
.
3. Рассчитать среднюю длину свободного пробега молекул азота, коэффициент диффузии и вязкость при давлении 
и температуре 
. Как изменятся найденные величины в результате двукратного увеличения объема газа при постоянном давлении? Эффективный диаметр молекул азота 
.
Дано: Найти:
, 
,
, 
,
, 
,
, 
, 
, 
.
.
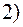
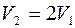Решение:
Средняя длина свободного пробега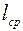 
и коэффициенты переноса и могут быть рассчитаны по формулам (8.9) и (8.10):
, (1)
, (2)
. (3)
Концентрацию молекул по заданным значениям давления и температуры можно определить из уравнения Клапейрона-Менделеева:
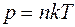. (4)
Выражения (1) - (3) имеют смысл, если длина свободного пробега, рассчитанная по формуле (1), много меньше линейных размеров сосуда. Поскольку начальное давление газа – атмосферное, можно утверждать, что это условие выполняется, хотя размеры сосуда и не оговорены в условии задачи.
Выражая концентрацию из уравнения (4) и подставляя ее в (1), можно получить:
.
Для расчета коэффициента диффузии по формуле (2) можно воспользоваться полученным результатом, определив предварительно среднюю скорость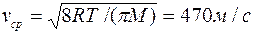 
. Тогда 
. Для расчета подставим в выражение (3) формулу (1):
,
где 
. Окончательно
. (5)
Как видно из выражения (1), длина свободного пробега зависит только от концентрации молекул. При двукратном увеличении объема концентрация уменьшается вдвое. Следовательно, при любом процессе
.
Индексы 1 и 2 соответствуют состояниям до и после расширения газа. В выражение коэффициента диффузии входит не только длина свободного пробега, но и средняя скорость. Следовательно,
.
При постоянном давлении объем прямо пропорционален термодинамической температуре: 
. Таким образом, 
.
Вязкость, как видно из выражения (5), зависит только от скорости молекул, следовательно, и от температуры (все остальные величины, входящие в выражение (5), постоянны), то есть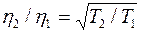 
. Это значит, что при постоянном давлении 
.
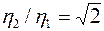Ответ: 
,
,
, , .
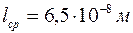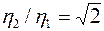