5.1. Система состоит из трех шаров с массами m1 = 1 кг, m2 = 2 кг, m3 = 3 кг, которые двигаются так, как показано на рисунке. Найдите величину скорости центра масс этой системы, если скорости шаров соответственно равны v1 = 3 м/с, v2 = 2 м/с, v3 = 1 м/с.

[Ответ: 2/3]
5.2. В лодке массой m1 = 240 кг стоит человек массой m2 = 60 кг. Лодка плывет со скоростью v1 = 2 м/с. Человек прыгает с лодки в горизонтальном направлении со скоростью v = 4 м/с (относительно лодки). Найти скорость лодки после прыжка человека в двух случаях: 1) человек прыгает вперед по движению лодки и 2) в сторону, противоположную движению лодки.
[Ответ: 1 м/c; 3 м/c]
5.3. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека 60 кг, масса доски 20 кг. С какой скоростью (относительно пола) будет двигаться тележка, если человек пойдет вдоль доски со скоростью (относительно доски) 1 м/с?
[Ответ: 0,75 м/c]
5.4. На полу стоит тележка в виде длинной доски, снабженной легкими колесами. На одном конце доски стоит человек. Масса человека 60 кг, масса доски 20 кг. На какое расстояние d: 1) передвинется тележка, если человек перейдет на другой конец доски; 2) переместится человек относительно пола; 3) переместится центр масс системы тележка – человек относительно доски и относительно пола. Длина l доски равна 2 м.
[Ответ: 1,5 м; 0,5 м; 1,5 м, 0]
5.5. На ж/д платформе установлено орудие. Масса платформы с орудием M = 15 т. Орудие стреляет в верх под углом φ = 600 к горизонту в направлении пути. С какой скоростью v1 покатится платформа вследствие отдачи, если масса снаряда m = 20 кг и он вылетает со скоростью v2 = 600 м/с.
[Ответ: 0,4 м/c.]
5.6. Снаряд массой m = 10 кг обладал скоростью v = 200 м/с в верхней точке траектории. В этой точке он разорвался на две части. Меньшая массой m1= 3 кг получила скорость u1 = 400 м/с в прежнем направлении. Найти скорость u2 второй, большей части после разрыва.
[Ответ: 114 м/c]
5.7. В предыдущей задаче найти, с какой скоростью u2 и под каким углом φ2 к горизонту полетит большая часть снаряда, если меньшая полетит вперед под углом φ1 =600 к горизонту.
[Ответ: 250 м/c; -36,60]
5.8. Частица массы 1 г, двигавшаяся со скоростью  , испытала абсолютно неупругое
, испытала абсолютно неупругое  столкновение с другой частицей, масса которой 2 г и скорость
столкновение с другой частицей, масса которой 2 г и скорость  . Найти скорость образовавшейся частицы – вектор
. Найти скорость образовавшейся частицы – вектор  и его модуль, - если проекции векторов
и его модуль, - если проекции векторов 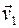 и
и  даны в системе СИ.
даны в системе СИ.
[Ответ:  ,
,  ]
]
5.9. Через неподвижный блок перекинута веревка, на одном конце которой висит лестница с человеком, а на другом – уравновешивающий груз массы М. Человек массы m совершил перемещение  относительно лестницы вверх и остановился. Пренебрегая массами блока и веревки, а также трением в оси блока, найти перемещение
относительно лестницы вверх и остановился. Пренебрегая массами блока и веревки, а также трением в оси блока, найти перемещение  центра масс этой системы.
центра масс этой системы.
[Ответ:  ]
]
5.10. Камень брошен вверх под углом φ =600 к плоскости горизонта. Кинетическая энергия камня в начальный момент времени равна 20 Дж. Определить кинетическую и потенциальную энергии камня в высшей точке его траектории. Сопротивлением воздуха пренебречь.
[Ответ: 5 Дж; 15 Дж.]
5.11. Тело массой 1 кг, брошенное с вышки в горизонтальном направлении со скоростью v0 = 20 м/с, через t =3 с упало на землю. Определить кинетическую энергию, которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.
[Ответ: 633 Дж.]
5.12. При выстреле из орудия снаряд массой m1 = 10 кг получает кинетическую энергию Т1 =1,8 МДж. Определить кинетическую энергию Т2 ствола орудия вследствие отдачи, если масса m2 ствола орудия равна 600 кг.
[Ответ: 30 кДж.]
5.13. В баллистический маятник массой М =5 кг попала пуля массой m =10 г и застряла в нем. Найти скорость пули, если маятник, отклонившись после удара, поднялся на высоту h =10 см.
[Ответ: 707 м/c.]
5.14. В точке максимального подъема снаряд, выпущенный из орудия вертикально вверх, разорвался на два осколка. Первый осколок массой m1, двигаясь вертикально вниз, упал на землю, имея скорость в 1,25 раза больше начальной скорости снаряда v0, а второй осколок массой m2 при касании поверхности земли имел скорость в 1,8 раз большую v0. Чему равно отношение масс m1/m2 этих осколков? Сопротивлением воздуха пренебречь.
[Ответ: 2.]
5.15. На горизонтальной поверхности лежит стальной кубик. В верхнюю грань кубика ударяется летящий по воздуху шарик, изготовленный из пластичного материала. Скорость шарика v0 в момент удара составляла угол α =300 с горизонтом. При столкновении 50% энергии шарика переходит в тепло, а сам шарик отражается от кубика и продолжает полет под некоторым углом β к горизонту с энергией в три раза меньшей первоначальной. Определите величину этого угла. Масса кубика в два раза больше массы шарика.
[Ответ: 600.]
5.16. Найти приращение кинетической энергии замкнутой системы из двух шариков с массами m1 и m2 при их абсолютно неупругом столкновении, если до столкновения скорости шариков были  и
и  .
.
[Ответ:  , где
, где 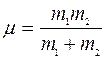 ]
]
5.17. Сплошной и полый (трубка) цилиндры, имеющие одинаковые массы и радиусы, вкатываются на горку с одинаковой начальной скоростью. Какой цилиндр поднимется выше? Найдите соотношение между высотой подъема сплошного цилиндра h1 и полого h2.
[ Ответ: h1 =0,75 h2 ]
5.18. На рисунке показан вектор силы, действующей на частицу. Найдите работу, совершаемую этой силой при перемещении частицы в точку с координатами (4;3).

[Ответ: 24 Дж]
5.19. Частица массы m движется по окружности радиуса R с нормальным ускорением, которое меняется со временем по закону  , где с – постоянная. Найти зависимость от времени мощности всех сил, действующих на частицу, а также среднее значение этой мощности за первые t секунд после начала движения.
, где с – постоянная. Найти зависимость от времени мощности всех сил, действующих на частицу, а также среднее значение этой мощности за первые t секунд после начала движения.
[ Ответ:  ]
]
5.20. Небольшое тело массы m находится в горизонтальной плоскости в точке О. Телу сообщили горизонтальную скорость  . Найти:
. Найти:
a) среднюю мощность, развиваемую силой трения за все время движения, если коэффициент трения  , m=1кг и
, m=1кг и  м/с;
м/с;
б) максимальную мгновенную мощность силы трения, если коэффициент трения меняется по закону  сx, где с - постоянная, x – расстояние от точки О.
сx, где с - постоянная, x – расстояние от точки О.
[Ответ:  ]
]
5.21. Невесомая доска покоится на двух опорах. Правая опора делит длину доски в отношении 1: 3. На ее правый конец падает тело массой m2 =2кг, скорость которого в момент удара v2. С какой скоростью начнет двигаться тело массой m1 =1кг, если после удара тело массой m2 =2кг полностью теряет свою скорость.
|

[Ответ: v1=6v2]
5.22. На краю горизонтальной платформы, имеющей форму диска радиусом R =2 м, стоит человек массой m1 =80 кг. Масса m2 платформы равна 240 кг. Платформа может вращаться вокруг вертикальной оси, проходящей через ее центр. Пренебрегая трением, найти, с какой угловой скоростью w будет вращаться платформа, если человек будет идти вдоль ее края со скоростью v =2 м/c относительно платформы.
[Ответ: 0,4 рад/c]
5.23. Платформа в виде диска радиусом R =1 м вращается по инерции с частотой n1 =6 мин-1. На краю платформы стоит человек, масса m которого равна 80 кг. С какой частотой n будет вращаться платформа, если человек перейдет в ее центр? Момент инерции J платформы равен 120 кг∙м2. Момент инерции человека рассчитать как для материальной точки.
[Ответ: 10 мин-1]
5.24. Найти наибольшее и наименьшее расстояние планеты А от Солнца С, если в некоторый момент времени она находилась на расстоянии  и имела скорость
и имела скорость 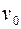 , причем угол между радиусом-вектором
, причем угол между радиусом-вектором  и вектором
и вектором  равен
равен  (см. рис).
(см. рис).
|

[Ответ:  , где
, где 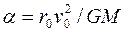 ]
]
5.25. Однородный шар радиуса r начинает скатываться без скольжения с вершины сферы радиуса R. Найти угловую скорость шара после отрыва от поверхности сферы.
[Ответ:  ]
]
§ 6. МОЛЕКУЛЯРНАЯ ФИЗИКА
Краткая теория
Идеальным называется газ, молекулы которого имеют пренебрежимо малый собственный объем и не взаимодействуют друг с другом на расстоянии. Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
 , (6.1)
, (6.1)
где р - давление; V – объем; T – термодинамическая температура; m – масса газа; M – молярная масса газа; R= 8,31 Дж/(моль∙К) – универсальная газовая постоянная; m/M = n – количество вещества.
Один моль любого газа содержит одно и то же число молекул NA, называемое постоянной Авогадро: NA = 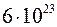 моль-1. Если m0 – масса одной молекулы, то масса произвольного количества вещества n равна
моль-1. Если m0 – масса одной молекулы, то масса произвольного количества вещества n равна
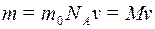 . (6.2)
. (6.2)
Молярным объемом называется величина Vm=V/n. Cогласно закону Авогадро, при одинаковых давлениях и температурах молярные объемы различных газов одинаковы.
Закон Бойля-Мариотта
pV=const при T=const, m=const. (6.3)
Закон Гей-Люссака
 , или
, или  при p=const, m=const. (6.4)
при p=const, m=const. (6.4)
Закон Шарля
p=p0 (1 +αt), или p/T=const при V=const, m=const, (6.5)
где t - температура по шкале Цельсия; V0 и p0 – соответственно объем и давление при 0 0 С; коэффициент  К-1.
К-1.
Основное уравнение молекулярно-кинетической теории идеальных газов
 , (6.6)
, (6.6)
где k – постоянная Больцмана (k=R/NA= 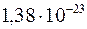 Дж/K), n – концентрация молекул газа (число молекул в единице объема n=N/V, где N - общее число молекул).
Дж/K), n – концентрация молекул газа (число молекул в единице объема n=N/V, где N - общее число молекул).






