Е1ср 
. (6.7)
Средняя кинетическая энергия молекулы
Eср 
, (6.8)
где i – число степеней свободы молекулы газа (сумма поступательных, вращательных и удвоенного числа колебательных степеней свободы (i = iпост+ iвращ+2 iколеб)). Для идеального газа iколеб =0, так как атомы в молекуле идеального газа жестко связаны друг с другом.
Для одноатомного идеального газа i= 3,
для двухатомного идеального газа i =5,
для трехатомного - i =6.
Закон Дальтона для давления смеси n идеальных газов:
, (6.9)
где pi – парциальное давление i - го компонента смеси.
Скорость молекул идеального газа:
Наиболее вероятная
vв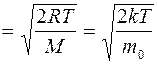 
; (6.10)
Средняя квадратичная
vср.кв . 
; (6.11)
Средняя арифметическая
vср 
. (6.12)
Закон Максвелла для распределения молекул идеального газа по скоростям:
f (v) 
, (6.13)
где функция f(v) распределения молекул по скоростям определяет относительное число молекул dN(v)/N из общего числа N молекул, скорости которых лежат в интервале от v до v+dv.
Закон Максвелла для распределения молекул идеального газа по энергиям теплового движения
, (6.14)
где функция f(E) распределения молекул по энергиям теплового движения определяет относительное число молекул dN(E)/N из общего числа N молекул, которые имеют кинетические энергии 
, заключенные в интервале от E до E+dE.
Барометрическая формула
, (6.15)
где ph и p0 – давление газа на высоте h и h0.
Уравнение состояния реальных газов (уравнение Ван-дер-Ваальса) для одного моля газа
(6.16)
Для произвольного количества вещества газа
, (6.17)
где а и b – постоянные Ван-дер-Ваальса (рассчитанные на один моль газа); V – объем, занимаемый газом; Vm – молярный объем; p – давление газа на стенки сосуда. Связь критических параметров – объема, давления и температуры газа – с постоянными а и b Ван-дер-Ваальса:
Vm кр= 
; 
; 
.
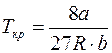Вопросы для самоподготовки
1. Сформулируйте основные постулаты молекулярно – кинетической теории газов.
2. Дайте определение идеального газа.
3. Дайте определение основным макроскопическим параметрам идеального газа: давлению, объему и температуре.
4. Напишите уравнение состояния идеального газа. Почему оно так называется?
5. Дайте определение постоянной Авогадро и молярной массе.
6. Сформулируйте Закон Авогадро. Чему равны молярные объемы всех газов при нормальных условиях?
7. Дайте определение процесса, изопроцесса.
8. Сформулируйте законы: Бойля – Мариотта, Гей–Люссака, Шарля. Постройте pV, pT, VT диаграммы для различных изопроцессов.
9. Назовите параметры, входящие в основное уравнение молекулярно-кинетической теории газов.
10. В чем отличие формул для средней кинетической энергии молекул одноатомного, двухатомного и трехатомного идеальных газов?
11. Сформулируйте закон Дальтона для давления смеси газов.
12. На рисунке представлен график функции распределения молекул идеального газа по скоростям (распределение Максвелла), где 
– доля молекул, скорости которых заключены в интервале скоростей от v до v+dv в расчете на единицу этого интервала.
Рис. 6.1. к вопросу №12.
Выберите верные утверждения.
а) Площадь заштрихованной полоски равна доле молекул со скоростями в интервале от v до v+dv.
б) С ростом температуры площадь под кривой растет.
в) С ростом температуры максимум кривой смещается вправо.
13. В трех одинаковых сосудах находится одинаковое количество газа, причем температуры газа в сосудах связаны соотношением: T1>T2>T3. Какая кривая будет описывать распределение скоростей молекул в сосуде с температурой T1?
14. Получите формулу для вычисления наиболее вероятной скорости (6.10), используя функцию распределения молекул идеального газа по скоростям (6.13).
15. Дайте определение средней квадратичной и средней арифметической скорости молекул газа. Покажите их на графике функции распределения молекул идеального газа по скоростям.
16. Используя барометрическую формулу, покажите графически изменение давления воздушного столба с высотой.
17. Напишите уравнения состояния для одного моля идеального и реального газов. В чем различие этих уравнений?
18. Изобразите pV диаграммы изотермического процесса для идеального и реального газа. Сделайте сравнительный анализ этих диаграмм.
Примеры решения задач
6.1. В сосуде находится смесь m1 =7 г азота и m2 =11 г углекислого газа при температуре Т =290 К и давлении р =1 атм. Найти плотность этой смеси, считая газы идеальными.
Дано: Найти:
m1 =7 г, 
.
m2 =11 г,
Т =290 К,
р =1 атм.
Решение:
Согласно закону Дальтона, давление р смеси газов равно сумме парциальных давлений азота р1 и углекислого газа р2:
. (1)
Для каждого газа, входящего в данную смесь, можно написать уравнение Клапейрона-Менделеева:
, 
. (2)
Выразив из уравнений (2) р1 и p2 и подставив в (1), можно получить:
. (3)
Объем сосуда можно представить в виде:
. (4)
Подставив (4) в (3), можно получить выражение для плотности смеси азота и углекислого газа:
кг/м3.
Ответ: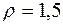 
кг/м3.
6. 2. Найти среднюю квадратичную скорость, среднюю кинетическую энергию поступательного движения и среднюю полную кинетическую энергию молекул гелия и азота при температуре 
. Определить полную энергию всех молекул 100 г каждого из газов.
Дано: Решение:
, 1) 
, 2) Еср.п
. 3) Еср.
4) Е
Решение:
Согласно равенству (6.7), средняя кинетическая энергия поступательного движения одной молекулы любого газа:
Дж, (1)
причем средние энергии поступательного движения молекулы гелия и азота одинаковы. Однако средняя квадратичная скорость молекул газа зависит от молярной массы 
его молекул:
, (2)
где 
. Для гелия 
, для азота 
.
Средняя полная энергия молекулы зависит не только от температуры, но и от структуры молекул – от числа 
степеней свободы:
. (3)
Гелий - одноатомный газ, следовательно, 
. Тогда по формуле (3) для гелия 
. Азот – двухатомный газ, следовательно, 
и 
.
Полная кинетическая энергия всех молекул, равная для идеального газа его внутренней энергии, может быть найдена, как произведение Еср на число N всех молекул:
E=Еср N. (4)
Очевидно,
, (5)
где 
- масса всего газа, отношение 
определяет число молей, а 
- постоянная Авогадро. Выражение (4) с учетом уравнения Клапейрона-Менделеева (6.1) позволит рассчитать полную энергию всех молекул газа:
. (6)
Для гелия 
; для азота 
.
Ответ: 1. 
, 
;
2. Дж;
3. 
, 
;
4. 
, 
.
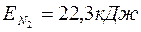3. Температура окиси азота NO T =300 K. Определить долю молекул, скорость которых лежит в интервале от v1 =820 м/c до v2 =830 м/c.
Дано: Найти:
T =300 K, 
.
v1 =820 м/c,
v2 =830 м/c.
Решение:
Рассматриваемый газ находится в равновесном состоянии, и, согласно распределению Максвелла, относительное число молекул, скорость которых заключена в интервале от v до v+dv:
,
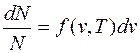где f(v,T) -функция Максвелла; dv - настолько малый диапазон скоростей, что в пределах его заведомо f(v,T)=const. В условии задачи требуется определить долю молекул, скорости которых лежат в диапазоне 
.
Если в диапазоне функцию Максвелла можно считать постоянной, то искомая величина может быть рассчитана по приближенной формуле:
. (1)
Такое приближение соответствует тому, что на рисунке 6.2 заштрихованная площадь приравнивается площади прямоугольника с основанием 
и высотой, равной значению f(v1,T). Следовательно, прежде всего надо найти значения функции Максвелла при v=v1 и v=v2 и выяснить, какую погрешность дает использование равенства (1).
Функцию Максвелла можно представить в виде:
, (2)
где
(3)
- наиболее вероятная скорость молекул. Тогда по формуле (2) можно найти f(v1,T) = 
с/м; f(v2,T) 
с/м.
Это значит, что при использовании выражения (1) допускается ошибка, относительная величина которой
.
Тогда доля молекул, скорость которых лежит в интервале от v1 =820 м/c до v2 =830 м/c можно найти по формуле (1) с точностью 7%:
.
Ответ: 
.
