Теплоемкость. Первое начало термодинамики

Краткая теория

Под теплоемкостью С понимают то количество тепла, которое надо сообщить телу, чтобы повысить его температуру на один градус Кельвина:

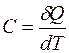. (7.1)

Если речь идет о передаче теплоты не всему телу, а одному килограмму, то говорят об удельной теплоемкости с=С/m (измеряется в Дж/(кг∙К)). Если речь идет о передаче теплоты одному молю вещества, то говорят о молярной теплоемкости C_µ = С/ν, измеряемой в Дж/(моль∙К).Связь между молярной (C_µ) и удельной (с) теплоемкостями газа:

 

(7.2)

где M – молярная масса газа.

Молярные теплоемкости газа при постоянном объеме и постоянном давлении соответственно равны (здесь и далее в целях упрощения записи в индексах обозначений молярной теплоемкости при постоянном давлении и постоянном объеме букву «µ» будем опускать):

 

C_V , C_p 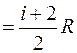, (7.3)

где i - число степеней свободы молекул газа; R= 8,31 Дж/(моль∙К) – универсальная газовая постоянная.

Уравнение Р. Майера

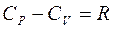. (7.4)

 

Показатель адиабаты

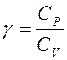, или . (7.5)

 

Внутренняя энергия идеального газа:

 

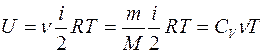, (7.6)

 

где Т – температура газа.

Политропическими называются процессы, при которых теплоемкость тела остается постоянной (С=const). Теплоемкость идеального газа при политропическом процессе:

, (7.7)

 

где n- показатель политропы. Изобарному процессу соответствует n=0, изотермическому n=1, изохорному n= , адиабатному n=g.

Внутренняя энергия реального газа

 

. (7.8)

где а – постоянная Ван-дер-Ваальса, V_m - молярный объем газа.

Работа, связанная с изменением объема газа, в общем случае вычисляется по формуле:

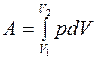, (7.9)

 

где V₁ – начальный объем газа; V₂ – его конечный объем, δA=pdV – элементарнаяработа газа при малом изменении объема dV.

Работа газа при изобарном процессе (p = const)

, или 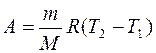; (7.10)

при изотермическом процессе (Т = const)

 

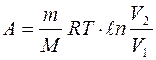, или ; (7.11)

при адиабатном процессе (адиабатным называется процесс, происходящий без обмена теплотой с окружающей средой)

, или 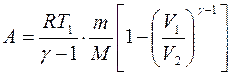, (7.12)

 

где Т₁ – начальная температура газа; Т₂ – его конечная температура.

Уравнение Пуассона (уравнение газового состояния при адиабатном процессе):

, , . (7.13)

 

Первое начало термодинамики:

 

, (7.14)

 

где Q – количество теплоты, сообщенное системе или отданное ею; 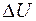- изменение ее внутренней энергии; A – работа системы против внешних сил.

Первое начало термодинамики для малого изменения системы:

 

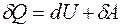. (7.15)

 

Первое начало термодинамики при изобарном процессе

, (7.16)

 

при изохорном процессе (А=0)

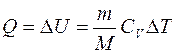
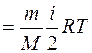, (7.17)

 

при изотермическом процессе ()

, (7.18)

 

при адиабатном процессе (Q=0)

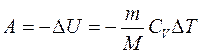
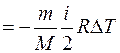. (7.19)

 

 

Вопросы для самоподготовки

 

1. Дайте определение теплоемкости тела, удельной и молярной теплоемкости вещества.

2. Как связаны между собой молярные теплоемкости при постоянном объеме и при постоянном давлении?

3. На рисунке схематически представлена температурная зависимость молярной теплоемкости при постоянном объеме C_V от температуры T для двухатомного газа. Назовите, какими степенями свободы обладают молекулы газа на участках 1-1^/, 2-2^/, 3-3^/. Почему на участках 1^/-2, 2^/-3 молярная теплоемкость газа изменяется?

 

 

Рис. 7.1 к вопросу №3

.

 

4. Дайте определение внутренней энергии.

5. Получите формулу (7.6) для внутренней энергии идеального газа.

6. Какой процесс называется адиабатным? Приведите примеры такого процесса.

7. Из уравнения Пуассона, связывающего давление и объем , и уравнения Клапейрона pV/T=const получите другие уравнения связи параметров состояния газа при адиабатном процессе и .

8. Сформулируйте первое начало термодинамики.

9. Примените первое начало термодинамики к изотермическому, изобарному, изохорному и адиабатному процессам.

10. Получите формулы для работы газа при изотермическом, изобарном и адиабатном процессах.

 

 

Примеры решения задач

 

7.1. Двухатомный идеальный газ, занимавший при давлении объем V₁= 4л, расширяют до объема V₂= 6л, при этом давление падает до значения р₂= 10⁵ Па. Процесс происходит сначала по адиабате, затем по изохоре. Определить работу газа, количество поглощенной теплоты и изменение внутренней энергии газа при этом переходе.

 

Дано: Найти:

, 1. А ₁₂,

V₁= 4л = 4∙10^-3 м³, 2. Q ₁₂,

V₂= 6л=6∙10^-3 м³, 3.Δ U ₁₂.

р₂= 10⁵ Па.

 

Решение:

 

Газ участвует в двух процессах: а) адиабатное расширение из состояния 1 в некоторое состояние B, в котором объем V_B=V₂, давление p_B неизвестно; б) изохорный переход из состояния B в состояние 2. Чтобы определить характер изохорного процесса – нагревание или охлаждение, - надо найти промежуточное значение давления p_B. Согласно уравнению Пуассона для адиабатного процесса (7.13)

 

. (1)

 

Газ двухатомный (число степеней свободы его молекулы i=5), следовательно, показатель адиабаты 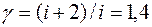. С учетом этого уравнение (1) примет вид:

. (2)

Неравенство (2) показывает, что при изохорном переходе из состояния B в состояние 2 давление газа уменьшается (рисунок 7.2) и, следовательно, процесс B-2 есть процесс изохорного охлаждения (p/T=const при V=const). Чтобы найти работу А₁₂ и количество поглощенной теплоты Q₁₂ при переходе из состояния 1 в 2, надо рассмотреть каждый из указанных процессов отдельно:

A₁₂=A_1B+A_B2, Q₁₂=Q_1B+Q_B2. (3)

 

Работа газа при адиабатном процессе:

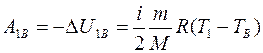. (4)

 

Уравнение Клапейрона - Менделеева для состояний 1 и В соответственно имеет вид:

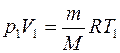, . (5)

Подставим уравнения (5) в (4) и найдем работу газа на участке 1В:

 

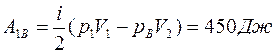. (6)

 

Учитывая, что 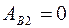, можно получить .

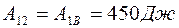На участке 1-В количество поглощенной теплоты Q_1B=0. На участке В-2 количество поглощенной теплоты можно найти из первого начала термодинамики для изохорного процесса:

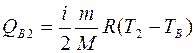. (7)

 

Подставляя уравнение Клапейрона - Менделеева для состояний В и 2 соответственно

,

в выражение (7), можно получить:

. (8)

 

Поскольку 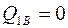, общее количество теплоты 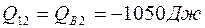. Знак минус показывает, что газ отдавал теплоту окружающим телам.

Изменение внутренней энергии не зависит от процесса и может быть определено по формуле (7.6), с использованием уравнения Клапейрона-Менделеева для состояний 1 и 2:

.

Ответ: 1. ,

2. ,

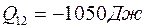3. .

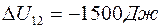7.2. Один моль идеального одноатомного газа нагревают от температуры Т₁= 150 К до Т₂= 400 К так, что в процессе нагрева р/V=const. Определить молярную теплоемкость и рассчитать количество теплоты, поглощенное газом при нагревании.

 

Дано: Найти:

, 1. C,

Т₁= 150 К, 2. Q.

Т₂= 400 К,

р/V=const.

 

Решение:

 

Запишем первое начало термодинамики в дифференциальной форме (7.15) для количества теплоты, поглощенного газом при нагревании:

 

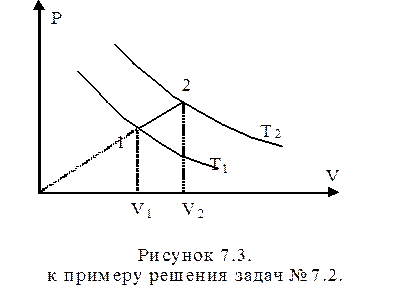
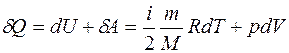. (1)

 

С другой стороны, по формуле для количества теплоты, переданного системе (7.1):

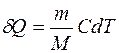, (2)

где С – молярная теплоемкость газа.

Приравнивая правые части выражений (1) и (2), получим выражение для молярной теплоемкости газа:

. (3)

 

Подставив выражение для давления, полученное из уравнения Клапейрона-Менделеева p=mRT/MV, поочередно в (3) и в уравнение процесса p/V=const, можно получить соответственно:

 

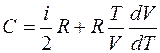, (4)

 

. (5)

 

Чтобы найти dV/dT, продифференцируем выражение (5) по переменной T:

 

,

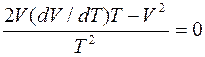откуда

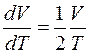. (6)

 

Подставив выражение (6) в (4), получим:

. (7)

Рассматриваемый газ – одноатомный (i=3). Тогда . Из формулы (7.1) найдем количество теплоты, поглощенное газом при нагревании:

 

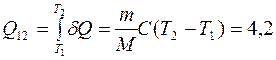кДж.

Ответ: 1. ,

2. Q₁₂= 4,2 кДж.

 

7.3. Найти работу, совершаемую одним молем ван-дер-ваальсовского газа при изотермическом расширении его от объема V₁ до V₂ при температуре T.

Дано: Найти:

, .

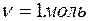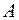V₁,

V₂,

T=const.

 

Решение:

Давление реального газа можно выразить из уравнения Ван-дер-Ваальса для одного моля газа:

. (1)

 

Подставив в формулу (7.9) выражение (1), можно найти работу, совершаемую одним молем ван-дер-ваальсовского газа при изотермическом расширении:

 

. (2)

 

После интегрирования получаем:

 

.

 

Ответ: .