3.1. Два бруска массами m1= 1 кг и m2= 4 кг, соединенные шнуром, лежат на столе. С каким ускорением а будут двигаться бруски, если к одному из них приложить силу F= 10 H, направленную горизонтально? Какова будет сила натяжения Т шнура, соединяющего бруски, если силу 10 Н приложить к первому бруску, ко второму бруску? Трением пренебречь.
[Ответ: 2 м/с2; 8 H; 2 H.]
3.2. На гладком столе лежит брусок массой m= 4 кг. К бруску привязаны два шнура, перекинутые через неподвижные блоки, прикрепленные к противоположным краям стола. К концам шнуров подвешены гири, массы которых m1= 1 кг и m2= 2 кг. Найти ускорение а, с которым движется брусок, и силу натяжения Т каждого из шнуров. Массой блоков и трением пренебречь.
[Ответ: 1,4 м/с2; Т1 =11,2 Н; Т2 =16,8 Н.]
3.3. Брусок массой m2= 5 кг может свободно скользить по горизонтальной поверхности без трения. На нем находится другой брусок массой m1= 1 кг. Коэффициент трения соприкасающихся поверхностей брусков μ =0,3. Определить максимальное значение силы Fmax, приложенной к нижнему бруску, при которой начнется соскальзывание верхнего бруска.
[Ответ: Fmax =17,7 Н.]
3.4. На горизонтальной поверхности находится брусок массой m1= 2 кг. Коэффициент трения μ1 бруска о поверхность равен 0,2. На бруске находится другой брусок массой m2= 8 кг. Коэффициент трения μ2 верхнего бруска о нижний равен 0,3. К верхнему бруску приложена сила F. Определить: 1) значение силы F1, при котором начнется совместное скольжение брусков по поверхности; 2) значение силы F2, при котором верхний брусок начнет проскальзывать относительно нижнего.
[Ответ: F1 = 19,6 Н; F2 =39,2 Н.]
3.5. Материальная точка массой m= 2 кг движется под действием некоторой силы F согласно уравнению 
, где С =1м/с2, D = -0,2 м/с3. Найти значение этой силы в моменты времени t1 =2с и t2 =5с. В какой момент времени сила равна нулю?
[Ответ: F1 = -0,8 Н; F2 = -8 Н; F =0 при t =1,67 с.]
3.6. Тело массой m движется в плоскости xy по закону x=Acosωt, y=Bsinωt, где A,B и ω - некоторые постоянные. Определить модуль силы, действующей на это тело.
[Ответ: F=mω2 
]
3.7. На горизонтальной плоскости с коэффициентом трения 
лежит тело массы m. В момент 
к нему приложили горизонтальную силу, меняющуюся со временем по закону 
где 
постоянный вектор. Найти путь, пройденный телом за первые 
секунд после начала действия этой силы.
[Ответ: 
где 
- момент начала движения.]
3.8. С вершины клина, длина которого l= 2 м и высота h =1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином μ= 0,15. Определить: 1) ускорение, с которым движется тело; 2) время прохождения тела вдоль клина; 3) скорость тела у основания клина.
[Ответ: 3,63 м/с2; 1,05 с; 3,81 м/c.]
3.9. По наклонной плоскости с углом наклона к горизонту, равным 300, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения μ= 0,15.
[Ответ: 7,26 м/c.]
3.10. На тело (рис.3.9) массой m= 10 кг, лежащее на наклонной плоскости (угол φ =200), начинает действовать горизонтально направленная сила F =8 Н. Пренебрегая трением, определить: 1) ускорение тела; 2) силу, с которой тело давит на плоскость.
[Ответы: 1) 4,11 м/с2; 2) 89,4 Н.]
3.11. Наклонная плоскость (рисунок 3.10) составляет угол φ =300 c горизонтом. Отношение масс тел 
. Коэффициент трения между телом m1 и наклонной плоскостью 
. Массы блока и нитей пренебрежимо малы. Найти модуль и направление ускорения тела m2, если система пришла в движение из состояния покоя.
[Ответ: 
.] 
3.12. Небольшой брусок начинает скользить по наклонной плоскости, составляющей угол φ c горизонтом. Коэффициент трения зависит от пройденного пути 
по закону 
, где 
постоянная. Найти путь, пройденный бруском до остановки, и максимальную скорость его на этом пути. [Указание. Чтобы привести уравнение движения к виду, удобному для интегрирования, надо представить ускорение как 
и затем произвести замену переменных по формуле 
.]
[Ответ: 
; 
.]
3.13. Грузик, привязанный к шнуру длиной 50 см, описывает окружность в горизонтальной плоскости. Какой угол φ образует шнур с вертикалью, если частота вращения n =1 с-1?
[Ответ: φ =60,20.]
3.14. Груз, привязанный к нити длиной 1 м описывает окружность в горизонтальной плоскости. Определить период Т обращения, если нить отклонена на угол φ =600 от вертикали.
[Ответ: 1,42 с.]
3.15. Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами m1 и m2 (например, m1>m2), которые подвешены на легкой нити, перекинутой через неподвижный блок (рис. 3.11). Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) силу натяжения нити Т; 3) силу F, действующую на ось блока.
[Ответ: 
, 
]
3.16. На рис. 3.12 изображена система блоков, к которым подвешены грузы массами m1= 200 г и m2= 500 г. Считая, что груз m1 поднимается, а неподвижный блок с m2 опускается, нить и блоки невесомы, силы трения отсутствуют, определить: 1) силу натяжения нити Т; 2) ускорения, с которыми движутся грузы.
[Ответ: 1) 2,26 Н; 2) а 1=1,5 м/c2, а 2=0,75 м/c2.]
3.17*. В установке (рисунок 3.13) известны масса стержня M и шарика m, причем M>m. Шарик имеет отверстие и может скользить по нити с некоторым трением. Массы блока и трение в его оси пренебрежимо малы. В начальный момент шарик находился напротив нижнего конца стержня. После того как систему предоставили самой себе, оба тела стали двигаться с постоянными ускорениями. Найти силу трения между шариком и нитью, если через t секунд после начала движения шарик оказался напротив верхнего конца стержня. Длина стержня равна 
.
[Ответ: 
.]
|
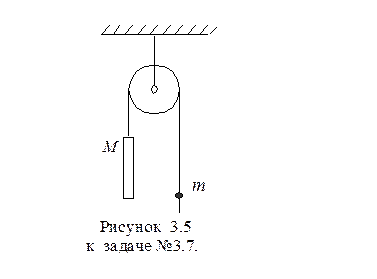
3.18. Самолет летит в горизонтальном направлении с ускорением а =20 м/с2. Какова перегрузка пассажира, находящегося в самолете? (Перегрузкой называется отношение силы F, действующей на пассажира, к силе тяжести Р.)
[Ответ: 2,27.]
3.19. Тело массой m =5 кг брошено под углом β =300 к горизонту с начальной скоростью v 0=20 м/с. Пренебрегая сопротивлением воздуха, найти: 1) импульс силы F, действующей на тело, за время его полета; 2) изменение Δ p импульса тела за время полета.
[Ответ: 1)100 Н∙c; 2) 100 кг∙м/c.]
3.20. Шарик массой m =300 г ударился о стену и отскочил от нее. Определить импульс p 1, полученный стеной, если в последний момент перед ударом шарик имел скорость v 0=10 м/с, направленную под углом β =300 к поверхности стены. Удар считать абсолютно упругим.
[Ответ: 3 Н∙c.]
3.21. На покоящуюся частицу массы m в момент времени t=0 начала действовать сила, зависящая от времени t по закону 
, где 
- постоянный вектор, τ – время, в течение которого действует постоянная сила. Найти:
1) импульс частицы после окончания действия силы;
2) путь, пройденный частицей за время действия силы.
[Ответ: 1) 
; 2) S=bτ4/ 12 m. ]
