МАТЕРИАЛЬНОЙ ТОЧКИ И ТВЕРДОГО ТЕЛА
Краткая теория
В качестве меры механического действия одного тела на другое в механике вводится векторная величина, называемая силой. В рамках классической механики имеют дело с гравитационными силами, а также с упругими силами и силами трения.
Сила гравитационного притяжения, действующая между двумя материальными точками, в соответствии с законом всемирного тяготения, пропорциональна произведению масс точек 
и 
, обратно пропорциональна квадрату расстояния 
между ними и направлена по прямой, соединяющей эти точки:
, (3.1)
где G =6,67∙10-11 м3/(кг∙с2) - гравитационная постоянная.
Сила тяжести – это сила притяжения в гравитационном поле небесного тела:
 ,
| (3.2) |
где 
- масса тела; 
- ускорение свободного падения, 
- масса небесного тела, - расстояние от центра масс небесного тела до точки, в которой определяется ускорение свободного падения (рис. 3.1).
Вес 
-это сила, с которой тело действует на опору или подвес, неподвижные относительно данного тела. Например, если тело с опорой (подвесом) неподвижны относительно Земли, то вес равен силе тяжести 
, действующей на тело со стороны Земли. В противном случае вес 
, где 
- ускорение тела (с опорой) относительно Земли.
Упругие силы
Всякое реальное тело под действием приложенных к нему сил деформируется, то есть изменяет свои размеры и форму. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Действующей на тело (пружину) силе противодействует упругая сила. С учетом направления действия для упругой силы 
имеет место формула:
 ,
| (3.3) |
где k - коэффициент упругости (жесткость в случае пружины),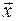 
- абсолютная деформация. Утверждение о пропорциональности между упругой силой и деформацией носит название закона Гука. Этот закон справедлив только для упругих деформаций.
В качестве величины, характеризующей деформацию стержня, естественно взять относительное изменение его длины:
, (3.4)
где l0- длина стержня в недеформированном состоянии, Δ l – абсолютное удлинение стержня. Опыт показывает, что для стержней из данного материала, относительное удлинение ε при упругой деформации пропорционально силе, приходящейся на единицу площади поперечного сечения стержня:
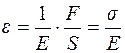, (3.5)
где E - модуль Юнга (величина, характеризующая упругие свойства материала). Эта величина измеряется в паскалях (1Па=1Н/м2). Отношение F/S представляет собой нормальное напряжение σ, поскольку сила F направлена по нормали к поверхности.
Силы трения
Придвижении телапо поверхности другого тела или в среде (воде, масле, воздухе и т.д.) оно встречает сопротивление. Это сила сопротивления движению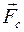 
. Она является результирующей сил сопротивления формы тела и трения: 
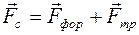. Сила трения 
всегда направлена вдоль поверхности соприкосновения в сторону, противоположную движению. Если имеется жидкая смазка, это будет уже вязкое трение между слоями жидкости. Аналогично обстоит дело и при движении тела, полностью погруженного в среду. Во всех этих случаях сила трения зависит от скорости сложным образом. Для сухого трения эта сила сравнительно мало зависит от скорости (при малых скоростях). Но трение покоя нельзя определить однозначно. Если тело покоится и нет силы, стремящейся сдвинуть тело,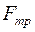 
равна нулю. Если такая сила есть, тело не сдвинется до тех пор, пока эта сила не станет равной некоторому значению 
, называемому максимальным трением покоя. Сила трения покоя может иметь значения от 0 до , что отражено на графике (рис. 3.2, кривая 1) вертикальным отрезком. В соответствии с рис. 3.2 (кривая 1), сила трения скольжения с увеличением скорости вначале несколько убывает, а затем начинает возрастать. Законы сухого трения сводятся к следующему: максимальная сила трения покоя, а также сила трения скольжения не зависят от площади соприкосновения трущихся тел и оказываются приблизительно пропорциональными величине силы нормального давления 
, прижимающей трущиеся поверхности друг к другу:
 ,
| (3.6) |
где 
- безразмерный коэффициент пропорциональности, называемый коэффициентом трения (соответственно покоя или скольжения). Он зависит от природы и состояния трущихся поверхностей, в частности от их шероховатости. В случае скольжения коэффициент трения является функцией скорости.
Трение качения подчиняется формально тем же законам, что и трение скольжения, но коэффициент трения в этом случае оказывается значительно меньшим.
Сила вязкого трения обращается в нуль вместе со скоростью. При малых скоростях она пропорциональна скорости:
, (3.7)
где 
- положительный коэффициент, характерный для данного тела и данной среды. Величина коэффициента зависит от формы и размеров тела, состояния его поверхности и от свойства среды, называемого вязкостью. Этот коэффициент зависит и от скорости 
, однако при малых скоростях во многих случаях его можно практически считать постоянным. При больших скоростях линейный закон переходит в квадратичный, то есть сила начинает расти пропорционально квадрату скорости (рис. 3.2, кривая 2).
Первый закон Ньютона: всякое тело находится в состоянии покоя или равномерного и прямолинейного движения, пока воздействие со стороны других тел не заставит его изменить это состояние.
Первый закон Ньютона утверждает, что состояние покоя или равномерного прямолинейного движения не требует для своего поддержания каких-либо внешних воздействий. В этом проявляется особое динамическое свойство тел, называемое инерцией. Соответственно первый закон Ньютона также называют законом инерции, а движение тела, свободного от внешних воздействий, - движением по инерции.
Опыт показывает, что всякое тело «оказывает сопротивление» при любых попытках изменить его скорость – как по модулю, так и по направлению. Это свойство, выражающее степень неподатливости тела к изменению его скорости, называется инертностью. У различных тел оно проявляется в разной степени. Мерой инертности служит величина, называемая массой. Тело с большей массой является более инертным, и наоборот. В рамках ньютоновской механики масса обладает следующими двумя важнейшими свойствами:
1) масса – величина аддитивная, то есть масса составного тела равна сумме масс его частей 
;
2) масса тела как такового – величина постоянная, не изменяющаяся при его движении.
Второй закон Ньютона: под действием результирующей силы тело приобретает ускорение
 ,
| (3.8) |
где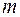 
- масса тела, 
- ускорение; 
- результирующая сила (геометрическая сумма сил, действующих на тело).
Третий закон Ньютона: каждой силе 
соответствует сила противодействия 
, равная по величине, но противоположно направленная:
 .
| (3.9) |
Силы и приложены к разным телам. Эти силы одной природы.
Импульс – векторная величина, равная произведению массы тела на его скорость:
 ,
| (3.10) |
где 
- импульс тела, 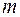- масса тела, 
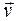- скорость тела.
Основное уравнение динамики поступательного движения для точки, входящей в систему точек:
, (3.11)
где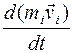 
- скорость изменения импульса i –ой точки системы; 
- сумма внутренних сил, действующих на i –ю точку со стороны всех точек системы; 
- результирующая внешняя сила, действующая на i –ю точку системы; N- число точек в системе.
Основное уравнение динамики поступательного движения для системы точек:
, (3.12)
где 
- скорость изменения импульса системы; 
- результирующая внешняя сила, действующая на систему.
Основное уравнение динамики поступательного движения твердого тела:
 ,
| (3.13) |
где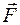 
- результирующая сила, действующая на тело; 
- скорость центра масс тела, 
скорость изменения импульса центра масс тела.
Вопросы для самоподготовки
1. Назовите группы сил в механике, дайте им определение.
2. Дайте определение результирующей силы.
3. Сформулируйте закон всемирного тяготения.
4. Дайте определение силы тяжести и ускорения свободного падения. От каких параметров зависят эти физические величины?
5. Получите выражение для первой космической скорости.
6. Расскажите о весе тела, условиях его изменения. Какова природа этой силы?
7. Сформулируйте закон Гука и укажите границы его применимости.
8. Расскажите о сухом и вязком трении. Объясните, как зависит сила сухого и вязкого трения от скорости движения тела.
9. Сформулируйте первый, второй и третий законы Ньютона.
10. Приведите примеры выполнения законов Ньютона.
11. Почему первый закон Ньютона называют законом инерции?
12. Дайте определение и приведите примеры инерциальных и неинерциальных систем отсчета.
13. Расскажите о массе тела как мере инертности, перечислите свойства массы в классической механике.
14. Дайте определение импульса тела и импульса силы, укажите единицы измерения этих физических величин.
15. Сформулируйте и запишите основной закон динамики поступательного движения для изолированной материальной точки, точки системы, системы точек и твердого тела.
16. Материальная точка начинает двигаться под действием силы Fx, график временной зависимости которой представлен на рисунке. Изобразите график отражающий зависимость величины проекции импульса px от времени.
Примеры решения задач
3. 1. Велосипедист едет по круглой горизонтальной площадке, радиус которой 
, а коэффициент трения зависит только от расстояния 
до центра 
площадки по закону 
где 
постоянная. Найти радиус окружности с центром в точке , по которой велосипедист может ехать с максимальной скоростью. Какова эта скорость?
Дано: Найти:
R, r(vmax), vmax.
Решение:
В задаче рассматривается движение велосипедиста по окружности. Так как скорость велосипедиста по модулю постоянна, то он движется с центростремительным ускорением 
под действием нескольких сил: силы тяжести 
, силы реакции опоры 
и силы трения 
(рис.3.4).
Применяя второй закон Ньютона, получим:
++ + = m . (1)
Выбрав оси координат (рис.1.3), запишем уравнение (1) в проекциях на эти оси:
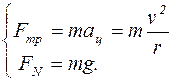
С учетом того, что Fтр=μFN= 
mg, получим выражение для скорости:
. (2)
Для нахождения радиуса r, при котором скорость велосипедиста максимальна, необходимо исследовать функцию v(r) на экстремум, то есть найти производную 
и приравнять ее к нулю:
= 
=0. (3)
Знаменатель дроби (3) не может быть равным нулю, тогда из равенства нулю числителя получим выражение для радиуса окружности, при котором скорость максимальна:
. (4)
Подставляя выражение (4) в (2), получим искомую максимальную скорость:
.
Ответ: 
.
На гладкой горизонтальной плоскости лежит доска массы m1 и на ней брусок массы m2. К бруску приложили горизонтальную силу, увеличивающуюся со временем по закону где c - постоянная. Найти зависимость от ускорения доски и бруска если коэффициент трения между доской и бруском равен. Изобразите примерные графики этих зависимостей.
Дано: Найти:
m1, 1. 
m2, 2. 
.
Решение:
|
|
|
В задаче рассматривается поступательное движение двух соприкасающихся тел (доски и бруска), между которыми действует сила трения. Между доской и плоскостью сила трения отсутствует. Сила F, приложенная к бруску, растет со временем, поэтому до некоторого момента времени 
брусок и доска движутся вместе с одинаковым ускорением, а при 
брусок начнет обгонять доску, будет скользить по ней. Сила трения всегда направлена в сторону, противоположную относительной скорости. Поэтому силы трения, действующие на доску 
и брусок 
, направлены так, как показано на рисунке 3.5, причем 
. Пусть момент начала отсчета времени t= 0совпадает с началом движения тел, тогда сила трения будет равна максимальной силе трения покоя 
(где 
сила нормальной реакции доски, уравновешенная силой тяжести бруска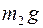 
). Ускорение доски 
возникает под действием одной силы трения , направленной так же, как и сила .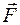
Зависимость ускорения доски и ускорения бруска от времени 
можно найти из уравнения второго закона Ньютона, записанного для каждого тела. Поскольку вертикальные силы, действующие на каждое из тел, скомпенсированы, то уравнения движения для каждого из тел можно записать в скалярной форме (для проекций на ось ОХ):
Учитывая, что 
, = 
, можно получить:
. (1)
Из системы уравнений (1) можно найти момент времени 
, учитывая, что при 
:
.
Решив систему уравнений (1) относительно 
, можно получить:
(при ). (2)
При ускорения 
и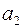 
различны, но сила трения имеет определенное значение 
, тогда:
(3)
|
График зависимости ускорений от времени для тел 
и 
можно построить на основании выражений (2) и (3). При график представляет собой прямую, выходящую из начала координат. При график 
прямая, параллельная оси абсцисс, график 
прямая, идущая вверх более круто (рис.3.6).
Ответ: при ускорения 
при 
. Здесь .
3.3. В установке (рисунок 3.7) известны угол φ наклонной плоскости с горизонтом и коэффициент трения между телом и наклонной плоскостью. Массы блока и нити пренебрежимо малы, трения в блоке нет. Считая, что в начальный момент оба тела неподвижны, найти отношение масс 
, при котором тело :
1) начнет опускаться;
2) начнет подниматься;
3) будет оставаться в покое.
Дано: Найти:
φ, 
Решение:
|
В задаче рассматриваются два тела, связанные нитью и совершающие поступательное движение. На тело массы действуют сила тяжести 
сила нормальной реакции наклонной плоскости, сила натяжения 
нити и сила трения . На тело действуют только сила тяжести 
и сила натяжения 
нити (рис. 3.7). В условиях равновесия ускорения первого и второго тела равны нулю 
, а сила трения является силой трения покоя, и ее направление противоположно направлению возможного движения тела . Применяя второй закон Ньютона для первого и второго тела, получаем систему уравнений:
(1)
Bследствие невесомости нити и блока 
. Выбрав оси координат (рис.3.7 а, 3.7 б), запишем для каждого тела уравнение движения в проекциях на эти оси. Тело начнет опускаться (рис. 3.7 а) при условии:
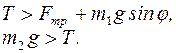
(2)
При совместном решении системы (2) можно получить
(3)
С учетом того, что 
выражение (3) можно записать в виде:
(4)
Тело начнет подниматься при условии (рис.3.7 б): 
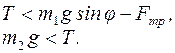(5)
При совместном решении системы (5) можно получить:
(6)
Тело будет находиться в покое при условии:
Ответ: 1) 
2) 
3) 
.
3.4. Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузы с массами и (
). Кабина начинает подниматься с ускорением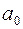 
. Пренебрегая массами блока и нити, а также трением, найти:
1) ускорение груза относительно шахты лифта и относительно кабины;
2) силу, с которой блок действует на потолок кабины.
Дано: Найти:
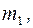1. 
2. 
.
.
Решение:
Грузы и движутся относительно кабины лифта и участвуют в движении лифта с ускорением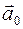 
. Если нить не растяжима, то ускорения грузов относительно кабины одинаковы по модулю и противоположны по направлению:
= 
.
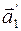Относительно шахты лифта ускорения грузов:
Для проекций на ось OY эти уравнения можно переписать в виде:
= 
(1)
Каждый из грузов движется под действием силы тяжести и силы натяжения нити. Параллельность сил, действующих на каждый из грузов, позволяет записать уравнения движения сразу в скалярной форме для проекций на ось OY:
(2)
Решая систему (1) относительно 
, можно получить:
. (3)
Подставляя (3) в систему уравнений (2), получим выражение для ускорения груза относительно шахты лифта:
.
Подставляя уравнения системы (1) в систему уравнений (2)
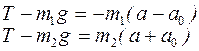(4)
и решая систему уравнений (4), можно получить выражение для ускорения груза относительно кабины лифта:
.
Сила давления блока на ось 
где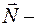 
сила реакции оси, действующая на блок и направленная вертикально вверх. Кроме этой силы на блок действуют силы натяжения нити, направленные вниз. Уравнение второго закона Ньютона для блока имеет вид:
где 
ускорение блока относительно Земли, 
его масса. Если 
то независимо от ускорения блока
Для проекций на ось OY данное уравнение можно переписать в виде:
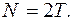
Уравнения (4) образуют систему с двумя неизвестными Т и а. Умножая первое уравнение этой системы на m2, а второе на m1 и складывая их почленно, можно получить:
.
Искомая сила давления блока на потолок кабины
, тогда
.
Ответ: 
, ;
.
