2.1. Снаряд вылетел со скоростью 
=320 м/c, сделав внутри ствола n=2 оборота. Длина ствола l =2 м. Считая движение снаряда в стволе равноускоренным, найти его угловую скорость вращения вокруг оси в момент вылета.
[Ответ: 
]
2.2. Якорь электродвигателя, имеющий частоту вращения 50 с-1, после выключения тока, сделав N =628 оборотов, остановился. Определить угловое ускорение якоря.
[Ответ: 12,5 рад/с2.]
2.3. Колесо автомашины вращается равнозамедленно. За время 2 минуты оно изменило частоту вращения от 240 до 60 мин-1. Определить число полных оборотов, сделанных колесом за это время.
[Ответ: 300.]
2.4. Диск радиусом R =10 см вращается так, что зависимость линейной скорости точек, лежащих на ободе диска, от времени задается уравнением v=At+Bt2 (A =0,3 м/с2, B =0,1 м/с3). Определить момент времени, для которого вектор полного ускорения образует с радиусом колеса угол φ =40.
[Ответ: 2с.]
2.5. Диск радиусом R =10 см вращается так, что зависимость угла поворота радиуса диска от времени задается уравнением φ=А+Bt3 (A =2 рад, B =4 рад/с3). Определить для точек на ободе колеса: 1) нормальное ускорение an в момент времени t =2c; 2) тангенциальное ускорение для этого же момента; 3) угол поворота φ, при котором полное ускорение составляет с радиусом колеса угол φ =450.
[Ответы: 1) 230 м/c2; 2) 4,8 м/c2; 3) 2,67 рад.]
2.6. Два твердых тела вращаются вокруг неподвижных взаимно перпендикулярных пересекающихся осей с постоянными угловыми скоростям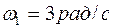и 
и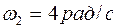 
. Найти угловую скорость одного тела относительно другого.
[Ответ: 
.]
2.7. Колесо вращается вокруг неподвижной оси так, что угол 
его поворота зависит от времени как 
где 
Найти полное ускорение 
точки А на ободе колеса в момент времени 
если линейная скорость точки А в этот момент 
[ Ответ: a=0,7 м/c2 ]
2.8. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением 
где 
Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол 
с ее вектором скорости?
[Ответ: t=7c ]
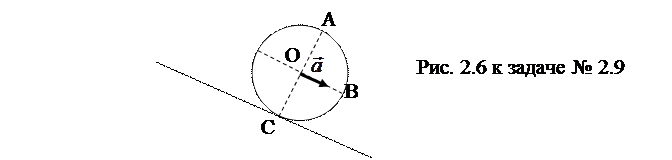
2.9. Шар радиусом R =10 см начинает скатываться без скольжения по наклонной плоскости так, что его центр движется с постоянным ускорением а =2,5 см/с2. Найти скорости и ускорения точек А, В и С относительно Земли в момент времени t =2 с, показанный на рис. 2.6.
[Ответы: vA= 10 см/c, aA =5,6 cм/c2; vB= 7 см/c, aB =2,5 cм/c2; vc= 0, ac =2,5 cм/c2.]
2.10. Твердое тело вращается вокруг неподвижной оси по закону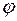 
= at-bt3, где a = 6 рад/c, b = 2 рад/с3. Найти:
1) среднее значение угловой скорости и углового ускорения за промежуток времени от t = 0 до остановки;
2) угловое ускорение в момент остановки тела. [Ответы: 1) 
; 2) 
. ]
2.11. Твердое тело вращается, замедляясь, вокруг неподвижной оси с угловым ускорением 
, где 
- его угловая скорость. Найти среднюю угловую скорость тела за время, в течение которого оно будет вращаться, если в начальный момент его угловая скорость была равна 
.
[Ответ: 
]
2.12. Твердое тело вращается вокруг неподвижной оси так, что его угловая скорость зависит от угла поворота j по закону 
, где и а – положительные постоянные. В момент t=0 угол 
. Найти зависимость от времени:
1) угла поворота;
2) угловой скорости.
[Ответы: 1) 
; 2) 
]
2.13. Твердое тело вращается с угловой скоростью 
где 
, 
и 
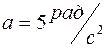орты осей X и Y. Найти угол φ между векторами углового ускорения 
и угловой скорости 
в момент, когда ε =10 рад/c2.
[Ответ: 190.]
2.14. Круглый конус с углом полураствора 
и радиусом основания R=5 см катится равномерно без скольжения по горизонтальной плоскости, как показано на рисунке 2.7. Вершина конуса закреплена шарнирно в точке О, которая находится на одном уровне с точкой С – центром основания конуса. Скорость точки С v=10 см/c. Найти модули:
1) вектора угловой скорости конуса и угол, который составляет этот вектор с вертикалью;
2) вектора углового ускорения конуса.
[Ответы:1) 
600;
2) 
]
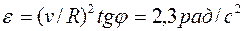