Краткая теория
Положение материальной точки или твердого тела при заданной оси вращения определяется углом поворота  или угловым перемещением
или угловым перемещением  , которое направлено вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта (рис. 2.1). Направление вектора поворота связывают с направлением вращения тела. Следовательно,
, которое направлено вдоль оси, вокруг которой вращается тело, в сторону, определяемую правилом правого винта (рис. 2.1). Направление вектора поворота связывают с направлением вращения тела. Следовательно,  является не истинным вектором, а псевдовектором.
является не истинным вектором, а псевдовектором.

Средняя угловая скорость и среднее угловое ускорение материальной точки
 ,
,  (2.1)
(2.1)
где  - изменение угла поворота за интервал времени
- изменение угла поворота за интервал времени  .
.
Мгновенная угловая скорость материальной точки
 . (2.2)
. (2.2)
Мгновенное угловое ускорение
 . (2.3)
. (2.3)
Направление векторов угловой скорости и углового ускорения совпадают с осью вращения (рис.2.1). Угловая скорость, угловое ускорение, как и угловое перемещение, являются псевдовекторами.
Частота вращения

 (2.4)
(2.4)
где  - число оборотов, совершаемых телом за время
- число оборотов, совершаемых телом за время 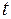 ;
; 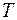 - период вращения (время одного полного оборота).
- период вращения (время одного полного оборота).
Число оборотов N, совершаемых телом при вращательном движении, связано с углом поворота φ соотношением:
N=2πφ. (2.5)
УРАВНЕНИЯ ОСНОВНЫХ ВИДОВ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Кинематическое уравнение равномерного вращательного движения
 , (2.6)
, (2.6)
где 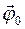 - начальное угловое перемещение;
- начальное угловое перемещение; 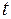 - время. При равномерном вращении
- время. При равномерном вращении 
Кинематическое уравнение равнопеременного вращательного движения (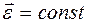 )
)
 , (2.7)
, (2.7)
где  - начальная угловая скорость.
- начальная угловая скорость.
Угловая скорость тела при равнопеременном вращательном движении
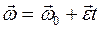 . (2.8)
. (2.8)
СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ, ХАРАКТЕРИЗУЮЩИМИ ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Длина пути, пройденного материальной точкой по дуге окружности радиусом  при повороте на угол Δ φ (рис.2.1)
при повороте на угол Δ φ (рис.2.1)
 . (2.9)
. (2.9)
Связь между линейной и угловой скоростью (рис.2.2)
 ;
;  . (2.10)
. (2.10)
Связь между тангенциальным и угловым ускорением (рис.2.2)

 . (2.11)
. (2.11)
Связь между нормальным ускорением и угловой скоростью
 -
-  (2.12)
(2.12)

ТАБЛИЦА АНАЛОГИЙ
| КИНЕМАТИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ | КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ |

| 
|
 
|  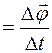
|
 
|  
|

| 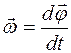
|

| 
|
 , при , при 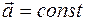
| 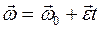 , при , при 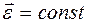
|
 , при , при 
| 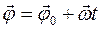 , при , при 
|
 , при , при 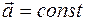
|  , при , при 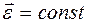
|
Вопросы для самоподготовки
1. Сформулируйте определение вращательного движения твердого тела.
2. Назовите основные кинематические характеристики вращательного движения, дайте им определение.
3. Объясните, почему линейное перемещение, скорость и ускорение не являются характеристиками вращательного движения твердого тела.
4. Дайте определение периода и частоты вращения.
5. Выведите кинематические уравнения равномерного и равнопеременного вращательного движения.
6. Выведите уравнение угловой скорости при равнопеременном вращательном движении.
7. Назовите формулы связи кинематических характеристик поступательного и вращательного движения.
8. Покажите аналогию между основными характеристиками поступательного и вращательного движения.
9. Материальная точка М движется по окружности со скоростью 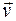 . На рисунке показан график зависимости проекции скорости vτ от времени (
. На рисунке показан график зависимости проекции скорости vτ от времени ( - единичный вектор положительного направления, vτ – проекция
- единичный вектор положительного направления, vτ – проекция 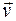 на это направление). Как при этом меняется величина нормального an и тангенциального a τ ускорения материальной точки?
на это направление). Как при этом меняется величина нормального an и тангенциального a τ ускорения материальной точки?
 |
Примеры решения задач
2.1. Материальная точка начинает двигаться по окружности радиуса r =10 см с постоянным касательным ускорением a τ=0,4 см/с2. Найти:
1) момент времени t от начала вращения, при котором вектор полного ускорения  образует с вектором скорости
образует с вектором скорости 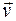 угол β= 450;
угол β= 450;
2) путь, пройденный материальной точкой за это время;
3) угол поворота материальной точки по окружности за это время.
Дано: Найти:
r =10 см; 1) t;
a τ=0,4 см/с2; 2) s;
β =450.3) φ.
Решение:
1. По условию задачи материальная точка движется по окружности с постоянным касательным ускорением  . Следовательно, мгновенную скорость движущейся точки при v0=0 можно найти по формуле (1.25), откуда
. Следовательно, мгновенную скорость движущейся точки при v0=0 можно найти по формуле (1.25), откуда
 .
.

Скорость v и нормальное ускорение an=v2/r непрерывно возрастают со временем, а вектор полного ускорения  со временем изменяется как по модулю, так и по направлению. Так как векторы
со временем изменяется как по модулю, так и по направлению. Так как векторы 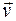 и
и  в данный момент времени всегда одинаково направлены, то угол β между векторами
в данный момент времени всегда одинаково направлены, то угол β между векторами  и
и 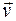 зависит от соотношения между нормальным an и касательным a τ ускорениями:
зависит от соотношения между нормальным an и касательным a τ ускорениями:
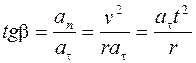 .
.
Тогда искомый момент времени найдем из соотношения:
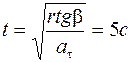 .
.
2. В соответствии с формулой (1.22) путь, пройденный материальной точкой за это время
 .
.
3. Угол поворота φ при вращательном движении линейно зависит от пройденного пути по формуле (2.9) и также изменяется со временем по квадратичному закону. Тогда угол поворота материальной точки в момент времени t =5c равен:
φ  .
.
Ответ: 1.  ; 2.
; 2.  ; 3. φ
; 3. φ 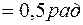 .
.
2.2. Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорением 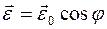 , где
, где  - постоянный вектор,
- постоянный вектор, 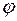 - угол поворота из начального положения. Найти угловую скорость тела в зависимости от угла
- угол поворота из начального положения. Найти угловую скорость тела в зависимости от угла 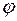 .
.
Дано: Найти:
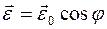 .
.  .
.
Решение:
Выберем положительное направление оси z вдоль вектора  . Согласно формуле (2.3),
. Согласно формуле (2.3),  . Представив dt по формуле (2.2) как
. Представив dt по формуле (2.2) как 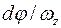 , можно преобразовать предыдущее уравнение к виду
, можно преобразовать предыдущее уравнение к виду
 . (1)
. (1)
Проинтегрируем выражение (1) с учетом начального условия ( ,
,  ):
):
 ;
;
 .
.
 .
.
Ответ:  .
.
2.3. Круглый конус с радиусом основания R и высотой h катится без скольжения по поверхности стола, как показано на рисунке 2.5. Вершина конуса закреплена шарнирно в точке О на уровне точки С – центра основания конуса. Точка С движется с постоянной скоростью v. Найти угловую скорость  .
.
Дано: Найти:
R,  .
.
h,
v.
Решение:
1. За промежуток времени dt цилиндр совершит поворот d  вокруг оси ОC и одновременно поворот d
вокруг оси ОC и одновременно поворот d 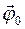 вокруг оси ОО/. Суммарный поворот
вокруг оси ОО/. Суммарный поворот  . Поделив обе части этого равенства на dt, получим
. Поделив обе части этого равенства на dt, получим
 , (1)
, (1)
где  и
и  - угловые скорости вращения вокруг осей ОО / и ОС соответственно. Модули векторов
- угловые скорости вращения вокруг осей ОО / и ОС соответственно. Модули векторов  и
и  можно найти, используя выражение (2.10):
можно найти, используя выражение (2.10): 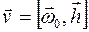 ,
, 
тогда 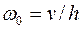 ,
,  . (2)
. (2)

|
Их отношение  . Модуль вектора
. Модуль вектора  можно найти по теореме Пифагора, используя выражения (2):
можно найти по теореме Пифагора, используя выражения (2):
 .
.
Ответ:  .
.




