Основные характеристики поступательного движения

A (x,y,z)

Положение материальной точки в пространстве (например, точки А(x,y,z)) задается радиус – вектором 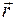, проведенным из начала координат в данную точку (рисунок 1.4).

	Рис.1.4. Наглядное изображение радиус – вектора материальной точки А (x,y,z).

Проекции радиус – вектора 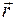на координатные оси равны декартовым координатам данной точки

 

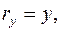
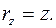
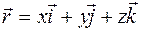, (1.9)

где 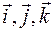- единичные векторы направлений (орты).

 

Средняя путевая скорость:

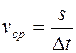, (1.10)

 

где - путь, пройденный точкой за интервал времени (рис.1.5).

Средняя скорость и среднее ускорение материальной точки:

, (1.11)

, (1.12)

где - перемещение материальной точки за интервал времени (рис.1.5).

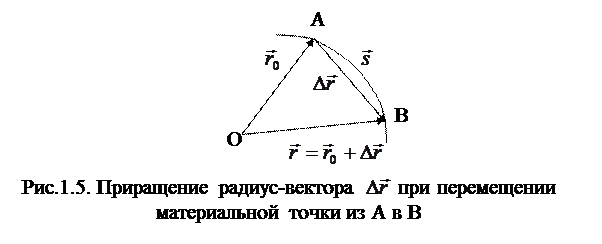
Мгновенная скорость материальной точки. Зафиксировав некоторый момент времени , рассмотрим приращение радиус – вектора за малый промежуток времени , следующий за (рис. 1.5).

Отношение 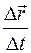дает среднее значение скорости за время . Если брать все меньшие промежутки , отношение 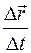в пределе дает значение скорости в момент времени :

(1.13)

Так как скорость векторная величина, то ее можно разложить на проекции:

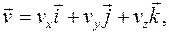(1.14)

где - проекции скорости на оси координат.

Модуль вектора скорости

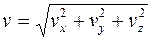. (1.15)

Мгновенное ускорение материальной точки

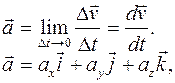(1.16)

где 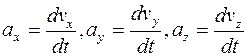- проекции ускорения 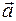на оси координат.

Модуль вектора ускорения

(1.17)

 

При криволинейном движении материальной точки удобно связать ее положение с центром скользящей системы координат – точкой С (рис.1.6) (τ и n – оси скользящей системы координат), тогда ускорение 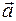можно представить как сумму нормальной и тангенциальной составляющих:

. (1.18)

 

Модули нормального, тангенциального и полного ускорения материальной точки:

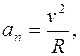(1.19)

(1.20)

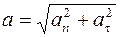, (1.21)

 

где R - радиус кривизны в данной точке траектории.

 

Путь, пройденный материальной точкой с момента времени t₁ до момента t₂:

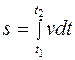, (1.22)

где v - модуль вектора скорости точки.

Кинематическое уравнение равномерного движения материальной точки

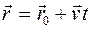, (1.23)

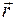где и радиус - векторы материальной точки в начальный и конечный моменты времени соответственно, 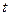- промежуток времени, соответствующий данному перемещению .

В координатной форме кинематическое уравнение прямолинейного равномерного движения примет вид:

 

r_x=r_ox+v_xt или 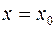+ v_xt.

При равномерном прямолинейном движении .

 

Кинематическое уравнение равнопеременного движения материальной точки

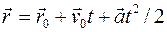, (1.24)

где - начальная скорость. При равнопеременном прямолинейном движении ускорение остается постоянным: .

В координатной форме уравнение равнопеременного прямолинейного движения материальной точки примет вид:

 

r_x=r_ox+v_0хt+a_xt²/2 или x = x₀ + v_0хt+a_xt²/2.