Прямолинейное движение
1.1. Рядом с поездом на одной линии с передними буферами паровоза стоит человек. В тот момент, когда поезд начал двигаться с ускорением a =0,1 м/с2, человек начал идти в том же направлении со скоростью v =1,5 м/с. Через какое время t поезд догонит человека? Определить скорость v1 поезда в этот момент и путь, пройденный за это время.
[Ответ: 30 c; 3 м/с; 45 м]
1.2. Тело, брошенное вертикально вверх, находилось на одной и той же высоте h =8,6 м два раза с интервалом Δ t =3 c. Пренебрегая сопротивлением воздуха, вычислить начальную скорость брошенного тела.
[Ответ:19,6 м/c]
1.3. Вертикально вверх подбросили шарик. На одной и той же высоте шарик побывал дважды: через 1,5 с и через 3,5 с после начала движения. Найдите начальную скорость шарика.
[Ответ: 20,5 м/c]
1.4. C балкона бросили мячик вертикально вверх с начальной скоростью v0 =5 м/с. Через t =2 с мячик упал на землю. Определить высоту балкона над землей и скорость мячика в момент удара о землю.
[Ответ: 9,62 м; 14,6 м/с]
1.5. Камень свободно падает без начальной скорости. За какое время камень пролетит третий метр своего пути?
[Ответ: 0,14 с]
1.6. Автомобиль, двигаясь при торможении равноускоренно, проходит за пятую секунду 5 см и останавливается. Какой путь прошел автомобиль за третью секунду этого движения?
[Ответ: 25 см]
1.7. Две материальные точки движутся согласно уравнениям:
X1=A1t + B1t2 + C1t3, X2= A2t + B2t2 + C2t3, где A1=4 м/с, B1=8 м/с2, C1= –16м/с3, A2=2 м/с, B2= –4 м/с2, C2=1 м/с. В какой момент времени t ускорения этих точек будут одинаковы? Найти скорости v1 и v2 точек в этот момент.
[Ответ: 0,235 c; 5,1 м/c; 0,286 м/c]
1.8. Точкапрошла половину пути со скоростью v0. На оставшейся части пути она половину времени двигалась со скоростью v1, а последний участок прошла со скоростью v2. Найти среднюю за все время движения скорость точки.
[Ответ: vср=2v0(v1+v2)/(2v0+v1+v2). ]
1.9. Точка движется вдоль оси Х со скоростью, проекция которой vx как функция времени описывается графиком на рис. 1.12. В момент t=0 координата точки x=0. Изобразить примерные графики зависимостей ускорения ах, координаты х и пройденного пути s от времени.
|
Криволинейное движение
1.10. Движение точки по кривой задано уравнениями x=A1t3 и y=A2t, где A1=1 м/с3 , A2=2 м/с. Найти уравнение траектории точки, ее скорость v и полное ускорение a в момент времени t =0,8 с.
[Ответ: y3-8x=0; 2,77 м/c; 4,8 м/c2]
1.11. Точка движется в плоскости xy по закону: x = bt, y = bt(1-nt), где b и n положительные постоянные, t – время. Найти:
1) уравнение траектории точки у(х); изобразить ее график;
2) скорость 
и ускорение 
точки в зависимости от времени;
3) момент t0, в который вектор скорости составляет угол 
с вектором ускорения.
[Ответы: 1) y=x-x2n/b; 2) 
; 3) t0=1/n. ]
1.12. Радиус-вектор, характеризующий положение частицы А относительно неподвижной точки О, меняется со временем по закону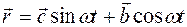 
, где 
и 
- постоянные векторы, причем ^ ; 
- положительная постоянная. Найти ускорение 
частицы и уравнение ее траектории у(х), взяв оси х и у совпадающими по направлению с векторами и соответственно и имеющими начало в точке О.
[Ответ: 
; 
.]
1.13. В момент t =0 частица вышла из начала координат в положительном направлении оси Х. Ее скорость меняется со временем t как 
, где 
-начальная скорость, ее модуль v0 =10 cм/с, τ=5 с. Найти:
1) координату х частицы, когда t =6, 10 и 20 с;
2) моменты времени, когда частица будет находиться на расстоянии 10 см от начала координат.
[Ответы: 1) 0,24; 0 и -2 м; 2) 1,1; 9 и 11 с.]
1.14. С вышки бросили камень в горизонтальном направлении. Через промежуток времени t =2 с камень упал на землю на расстоянии s =40 м от основания вышки. Определить начальную v0 и конечную v скорости камня.
[Ответ: 20 м/c; 28 м/c]
1.15. Тело, брошенное с башни в горизонтальном направлении со скоростью v =20 м/с, упало на землю на расстоянии S (от основания башни), вдвое большем высоты h башни. Найти высоту башни.
[Ответ: 20,4 м]
1.16. Самолет, летевший на высоте h =2940 м со скоростью v =360 км/ч, сбросил бомбу. За какое время t до прохождения над целью и на каком расстоянии S от нее должен самолет сбросить бомбу, чтобы попасть в цель? Сопротивлением воздуха пренебречь.
[Ответ: 24,5 с; 2,45 км]
1.17. Тело брошено под некоторым углом ά к горизонту. Найти этот угол, если горизонтальная дальность s полета тела в четыре раза больше максимальной высоты H траектории.
[Ответ: 450]
1.18. Два шарика бросили одновременно из одной точки в горизонтальном направлении в противоположные стороны со скоростями 
=3 м/cи 
=4 м/c. Найти расстояние между шариками в момент, когда их скорости окажутся взаимно перпендикулярными.
[Ответ: 
м.]
1.19. Из пушки выпустили последовательно два снаряда со скоростью 
=250 м/c: первый – под углом 
=600 к горизонту, второй – под углом 
=450 (азимут один и тот же). Пренебрегая сопротивлением воздуха, найти интервал времени между выстрелами, при котором снаряды столкнутся друг с другом.
[Ответ: 
]
1.20. Камень брошен с вышки в горизонтальном направлении с начальной скоростью 
Определить скорость 
тангенциальное 
и нормальное 
ускорения камня в конце второй секунды после начала движения.
[Ответы: v=35,8 м/c; at=5,37м/c2; an=8,22м/c2. ]
1.21. Тело брошено под углом 
к горизонту. Найти тангенциальное и нормальное ускорения в начальный момент движения.
[Ответы: at=4,9 м/c2; an=8,55м/c2. ]
1.22. Воздушный шар начинает подниматься с поверхности Земли. Скорость его подъема постоянна и равна . Благодаря ветру шар приобретает горизонтальную компоненту скорости 
by, где b - постоянная, y- высота подъема. Найти зависимость от высоты подъема:
1) величины сноса шара х(у);
2) полного, тангенциального и нормального ускорения шара. [Ответы: 1) x=(b/ 2v0)y2;2) a=bv0, 
. ]
1.23. Частица движется в плоскости ху со скоростью 
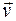= c 
+ bx 
где и 
- орты осей X и Y, c и b – положительные постоянные. В начальный момент частица находилась в начале координат. Найти:
1) уравнение траектории частицы у(х);
2) радиус кривизны траектории как функцию х.
[Ответы: 
.]
1.24. Шарик начал падать с нулевой начальной скоростью на гладкую наклонную плоскость, составляющую угол 
с горизонтом. Пролетев расстояние h, он упруго отразился от плоскости. На каком расстоянии от места падения шарик отразился второй раз?
[Ответ: l=8hsina ]
Относительность движения
1.25. Ученик наблюдал за встречным движением скорого поезда и электрички. Оказалось, что каждый из поездов прошел мимо мальчика за одно и тоже время t1=23 c. А в это время пассажир ехал в электричке и определил, что скорый поезд прошел мимо него за t2=13 c. Во сколько раз скорый поезд длиннее электрички?
[Ответ: 1,3. ]
1.26. Корабль движется по экватору на восток со скоростью v0 =30 км/ч. С юго-востока под углом φ =600 к экватору дует ветер со скоростью v =15 км/ч. Найти скорость v/ ветра относительно корабля и угол φ/ между экватором и направлением ветра в системе отсчета, связанной с кораблем.
[Ответы: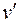 
=40 км/ч, φ/ =190.]
1.27. Лодка движется относительно воды со скоростью, в n = 2 раза меньшей скорости течения реки. Под каким углом к направлению течения лодка должна держать курс, чтобы ее снесло течением как можно меньше?
[Ответ: 
]
1.28. От бакена, который находится на середине широкой реки, отошли две лодки, А и В. Обе лодки стали двигаться по взаимно перпендикулярным прямым: лодка А – вдоль реки, а лодка В – поперек. Удалившись на одинаковое расстояние от бакена, лодки вернулись затем обратно. Найти отношение времен движения лодок τА/τВ, если скорость каждой лодки относительно воды в n =1,2 раза больше скорости течения.
[Ответ: τА/τВ = n/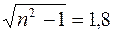 
. ]
