5.1 Поняття майбутньої і теперішньої вартості.
Однією з основоположних концепцій проектного аналізу є концепція вартості грошей в часі, яку було сформовано Ірвінгом Фішером. Ця концепція тісно пов'язана з концепцією альтернативної вартості і дає підстави для міркування про те, якою мірою вкладення відповідають інтересам власників.
Вартість грошей у часі – це норма прибутковості, що відображає цінність розпорядження грошима протягом певного періоду часу, як правило, року. Тобто це прибутковість, яку повинні принести гроші для того, щоб вони себе виправдали з погляду інвестора.
З часом економічні умови в країні змінюються, змінюється цінність володіння грошовими коштами, а, отже, змінюється і вартість грошей в часі.
Вартість грошей залежить від різних чинників. По-перше, від альтернативних можливостей вкладення капіталу, тому вартість грошей не може бути нижче за ставку по депозитах в банку, а в країні з розвиненим ринком цінних паперів – прибутковості по низькоризиковим цінним паперам.
По-друге, від рівня інфляції в економіці. Цей чинник надає безпосередній вплив на попередній – ставка по депозитах коректується на рівень інфляції. Тому при прогнозуванні вартості грошей для довгострокових проектів має бути зроблено прогноз інфляції.
По-третє, на вартість грошей впливає ступінь ризику. Ступінь ризику залежить від особливостей кожного конкретного проекту, його тривалості, галузі в якій він реалізується, а також від політичної і економічної ситуації в країні в цілому.
Вартість грошей в часі виражається у вигляді процентної ставки.
Процентна ставка – вимірювання вартості грошей в часі, що відображає прибутковість, яку міг би отримати інвестор. Розрізняють дві схеми нарахування відсотків: прості відсотки і складні відсотки.
При використанні схеми простих відсотків дохід на інвестовану суму нараховується виходячи тільки з початкової суми інвестицій. При цьому, сума, яку зможе отримати інвестор через певний період часу, розраховуватиметься за наступною формулою.
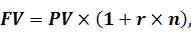(5.1)
де FV – майбутня вартість;
PV – теперішня вартість;
r – процентна ставка, яку виражено у коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Майбутня вартістьгрошей FV (Future Value) - це сума грошей, яка буде отримана від інвестиції через певний період часу з урахуванням певної процентної ставки, тобто це вартість інвестицій в майбутньому.
При використанні схеми складних відсотків дохід нараховується не тільки на суму інвестицій, але і на нараховані раніше відсотки. У проектному аналізі для розрахунку майбутньої вартості використовується схема нарахування складних відсотків, оскільки проектний аналіз засновано на виборі найкращої з можливих альтернатив. Майбутня вартість в проектних розрахунках визначається за наступною формулою.
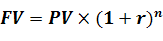(5.2)
де FV – майбутня вартість;
PV – теперішня вартість;
r – процентна ставка, виражена в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Процес розрахунку майбутньої вартості називається компаундуванням. Іноді використовуються синоніми компаундинг, нарощування.
Компаундування - процес розрахунку майбутньої вартості первинної грошової суми через певний проміжок часу з використанням певної ставки відсотка.
Процентна ставка, яка використовується при розрахунку майбутньої вартості, називається ставкою компаундування. А значення, на яке помножується теперішня вартість, називається фактором майбутньої вартості, або коефіцієнтом компаундування і позначається FVIF (Future Value Interest Factor), який розраховується за наступною формулою.
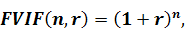(5.3)
де FVIF (n,r) – коефіцієнт компаундування, якщо процентна ставка дорівнює r, а період інвестування - n;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Таким чином, якщо підставити формулу (5.3) до формули (5.2), можна розрахувати майбутню вартість так.
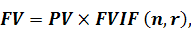(5.4)
де FV – майбутня вартість;
PV – теперішня вартість;
FVIF(n,r) – коефіцієнт компаундування, якщо процентна ставка дорівнює r, а період інвестування - n.
Для полегшення розрахунків можна скористатися таблицею стандартних значень FVIF, в якій FVIF визначається на перетині кількості років і процентної ставки, на яких здійснюється інвестиція.
Якщо інвестиції здійснюються не на цілий період, а на його частину, розрахунок майбутньої вартості здійснюється за наступною формулою.
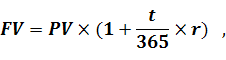(5.5)
де t - кількість днів, на які здійснюється інвестиція;
FV – майбутня вартість;
PV – теперішня вартість;
r – процентна ставка, яку виражено в коефіцієнтній формі.
Якщо відсотки на інвестиції нараховуються кілька разів за період (рік), розрахунок майбутньої вартості виконується за наступною формулою:
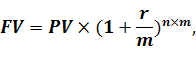(5.6)
де FV – майбутня вартість;
PV – теперішня вартість;
r – процентна ставка, виражена в коефіцієнтній формі;
m - кількість нарахувань за період, од.
Якщо протягом терміну проекту ставка відсотку змінюватиметься, то майбутня вартість буде розраховуватися за наступною формулою.
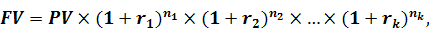(5.7)
де FV – майбутня вартість;
PV – теперішня вартість;
r – процентна ставка, яку виражено в коефіцієнтній формі;
k – кількість варіантів процентної ставки.
Однією з ознак проекту є його тривалість у часі. Тобто між моментом первинних інвестицій і моментом отримання останнього результату протікає певний часовий проміжок, іноді досить значний. Протягом цього проміжку часу вартість грошей постійно змінюється. А, отже, порівнювати вигоди і витрати різних років без приведення їх до зіставного вигляду некоректно. Це все одно, що підсумовувати сантиметри і метри, не перевівши одні до інших. Вартість грошей сьогодні більше, ніж в майбутньому, оскільки у майбутньому первинна сума збільшується за рахунок процентної ставки. Для того, щоб привести грошові потоки різних років до зіставного вигляду використовується процедура дисконтування.
Дисконтування - процес розрахунку теперішньої вартості грошових сум, які відносяться до майбутніх періодів часу.
Теперішня вартість грошей – це вартість майбутніх грошових потоків готівки, які дисконтовані за відповідною ставкою.
Розрахунок теперішньої вартості проводиться за наступною формулою.
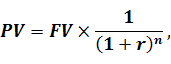(5.8)
де PV – теперішня вартість;
FV – майбутня вартість;
r – процентна ставка, виражена в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Коефіцієнт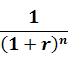 
має декілька назв – коефіцієнт дисконтування, коефіцієнт приведення теперішньої вартості, чинник теперішньої вартості і позначається PVIF (Present Value Interest Factor).
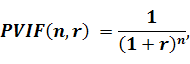(5.9)
де PVIF (n,r) – коефіцієнт дисконтування, якщо процентна ставка дорівнює r, а період інвестування - n;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Тобто, визначити теперішню вартість можна, підставивши формулу (5.9) до формули (5.8).
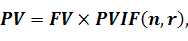(5.10)
де PV – теперішня вартість;
FV – майбутня вартість;
PVIF (n,r) – коефіцієнт дисконтування, якщо процентна ставка дорівнює r, а період інвестування - n.
Для полегшення розрахунків можна скористатися таблицею стандартних значень PVIF.
Однією з основних проблем при дисконтуванні грошових потоків є обґрунтування ставки дисконтування r (іноді говорять «ставки дисконту»). Існує дві основні точки зору на вибір ставки дисконтування. Так, вибір може ґрунтуватися на прибутковості альтернативних можливостей використання капіталу аналогічного ступеню ризику. Так, наприклад, якщо в середньому на підприємстві прибутковість по проектах складає 22%, то і ставка дисконтування аналізованого проекту має бути не менше 22 %. Якщо ризик аналізованого проекту вище чим середній рівень ризику проектів підприємства, то і ставка дисконтування має бути вище. Іноді, ставка дисконтування вибирається як середня прибутковість в галузі або в країні.
Другий підхід до вибору ставки дисконтування заснований на ціні, яку платить замовник за використання ресурсів. Тобто, на вибір ставки дисконтування робить вплив те, які джерела фінансування є у підприємства.
В процесі оцінки проектів необхідно зупиниться на одному способі приведення грошових потоків до зіставного вигляду – або дисконтування, або компаундування. Як правило, використовується метод дисконтування, і всі грошові потоки приводять у відповідність з нульовим роком (роком здійснення первинних інвестицій). При використанні компаундування всі грошові потоки приводять до останнього року.
Для того, щоб оцінити прибутковість інвестування при відомих значеннях теперішньої і майбутньої вартостей, необхідно перетворити формулу компаундування.
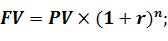
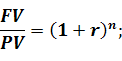
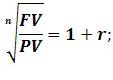
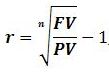(5.11)
де r – процентна ставка, яку виражено в коефіцієнтній формі;
FV – майбутня вартість;
PV – теперішня вартість;
n – кількість періодів, на які здійснюються інвестиції.
5.2 Визначення ануїтету.
Ануїтет - однонаправлений грошовий потік, який здійснюється через рівні проміжки часу в рівному розмірі.
Ануїтет пренумерандо, або авансові платежі– це грошовий потік, який здійснюється через рівні проміжки часу в рівному розмірі на початку періоду.
Наприклад, підприємство планує придбати будівлю під офіс і з цією метою на початку кожного року здійснює внески рівними сумами.
Для оцінки майбутньої вартості ануїтету пренумерандо використовують наступну формулу:
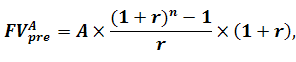(5.12)
де FVApre - майбутня вартість ануїтету пренумерандо;
А - сума ануїтету;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Для оцінки теперішньої вартості ануїтету пренумерандо використовують наступну формулу:
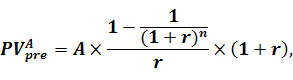(5.13)
де PVApre - теперішня вартість ануїтету пренумерандо;
А - сума ануїтету;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Ануїтет постнумерандо - грошовий потік, який здійснюється через рівні проміжки часу в рівному розмірі наприкінці періоду.
Наприклад, підприємство придбало автомобіль в кредит, який погашає рівними сумами в кінці року.
Для оцінки майбутньої вартості ануїтету постнумерандо використовують наступну формулу:
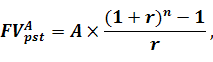(5.14)
де FVApst - майбутня вартість ануїтету постнумерандо;
А - сума ануїтету;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Для полегшення розрахунків можна скористатися таблицею стандартних значень FVIFA - чинника майбутньої вартості ануїтету, який розраховується за наступною формулою:
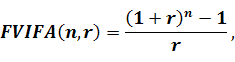(5.15)
де FVIFA (n,r) - чинник майбутньої вартості ануїтету;
r – процентна ставка, виражена в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Підставивши формулу (5.15) до формули (5.14), процес розрахунку майбутньої вартості можна представити за допомогою наступної формули:
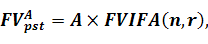(5.16)
де FVApst - майбутня вартість ануїтету постнумерандо;
А - сума ануїтету;
FVIFA(n,r) - чинник майбутньої вартості ануїтету, якщо процентна ставка дорівнює r, а період інвестування - n.
Для оцінки теперішньої вартості ануїтетупостнумерандо використовують наступну формулу:
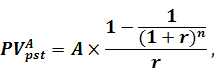(5.17)
де PVApst - теперішня вартість ануїтету постнумерандо;
А - сума ануїтету;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Для полегшення розрахунків можна скористатися таблицею стандартних значень PVIFA - чинника теперішньої вартості ануїтету, який розраховується за наступною формулою:
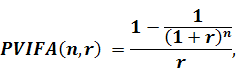(5.18)
де PVIFA (n,r) - чинник теперішньої вартості ануїтету, якщо процентна ставка дорівнює r, а період інвестування - n;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Якщо підставити формулу (5.18) до формули (5.17), процес розрахунку майбутньої вартості можна представити за допомогою наступної формули:
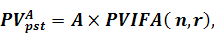(5.19)
де PVApst - теперішня вартість ануїтету постнумерандо;
А - сума ануїтету;
PVIFA (n,r)- чинник теперішньої вартості ануїтету, якщо процентна ставка дорівнює r, а період інвестування - n;
У тому випадку, коли існує необхідність визначити суму ануїтету, його виводять з формули дисконтування або компаундування.
Так, якщо необхідно визначити суму ануїтету на основі інформації про майбутню вартість ануїтету постнумерандо, використовують наступну формулу.
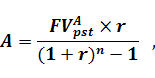(5.20)
де FVApst - майбутня вартість ануїтету постнумерандо;
А - сума ануїтету;
r – процентна ставка, яку виражено в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
Якщо наведено дані про теперішню вартість ануїтету постнумерандо, суму ануїтету визначають за наступною формулою.
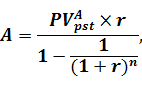(5.21)
де PVApst - теперішня вартість ануїтету постнумерандо;
А - сума ануїтету;
r – процентна ставка, виражена в коефіцієнтній формі;
n – кількість періодів, на які здійснюються інвестиції.
5.3 Урахування інфляції в проектних розрахунках.
Проблема урахування інфляції є важливою в проектних розрахунках, особливо в країнах з гіперінфляцією або галопуючою інфляцією.
Захистити дохід інвестора від дії інфляції можна, якщо включати в ставку дисконтування інфляційну премію.
Інфляційна премія(IP) – це надбавка до ставки прибутковості, яку спрямовано на нівелювання дії інфляції на дохід інвестора.
Інфляційну премію можна представити таким чином.
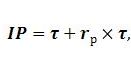(5.22)
де IP – інфляційна премія, яку виражено в коефіцієнтній формі;
rp – реальна процентна ставка, яку виражено в коефіцієнтній формі;
τ – темп інфляції в економіці у коефіцієнтній формі.
У формулі (5.22) вживання значення темпу інфляції τ забезпечує урахування дії інфляції на суму інвестицій в інфляційній премії, а значення r×τ - урахування дії інфляції на суму доходу,що отримується (дія інфляції на відсотки, що нараховуються).
Реальна процентна ставка (реальна прибутковість) – це прибутковість, яку очищено від дії інфляції. Тобто, це прибутковість, яку дійсно планує отримати інвестор, яку він заробив би, якби ціни залишалися незмінними.
Коли інвестор обгрунтовує ставку дисконтування, він завжди повинен враховувати інфляцію – закладати інфляційну премію.
Якщо ставка прибутковості менше темпу інфляції, тобто r<τ, то інвестор втрачає більше, ніж вкладає – інфляція знецінює не тільки отриманий дохід, але і частину або всю суму інвестицій.
Якщо ставка прибутковості дорівнює темпу інфляції, тобто r=τ, то інфляція знецінює повністю дохід інвестора, проте не впливає на суму інвестицій.
Якщо ставка прибутковості більше за темп інфляції, тобто r>τ, то інвестор отримує дохід від інвестиції – інфляція знецінює тільки частину доходу. Яку частину доходу знецінює інфляція, залежить від рівня інфляції і рівня номінальної прибутковості.
Номінальна прибутковість (номінальна процентна ставка) – це прибутковість, яка не враховує знецінення доходу інвестора під впливом інфляції. Тобто, із значення номінальної процентної ставки неможливо зрозуміти, скільки дійсно заробляє інвестор, а скільки знецінюється під впливом інфляції.
Для того, щоб нівелювати вплив інфляції на прибутковість, необхідно до прибутковості, яку планує інвестор, додати інфляційну премію.
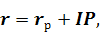(5.23)
де r – номінальна дохідність у коефіцієнтній формі;
rp – реальна процентна ставка, яку виражено у коефіцієнтній формі;
IP – інфляційна премія, яку виражено у коефіцієнтній формі.
Тобто, якщо підставити формулу (5.22) до формули (5.23), номінальну ставку відсотка можна визначити за наступною формулою.
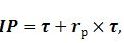(5.24)
де r – номінальна дохідність у коефіцієнтній формі;
rp – реальна процентна ставка, яку виражено у коефіцієнтній формі;
τ – темп інфляції в економіці у коефіцієнтній формі.
З формули (5.23) можна вивести формулу, згідно якій можна визначити реальну прибутковість на основі даних про номінальну прибутковість і темп інфляції.
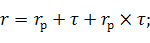
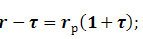
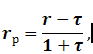(5.25)
де rp – реальна процентна ставка, яку виражено у коефіцієнтній формі;
r – номінальна дохідність у коефіцієнтній формі;
τ – темп інфляції в економіці у коефіцієнтній формі.
Для того, щоб оцінити, чому б дорівнювада майбутня вартість, якби ціни не змінювалися, використовується поняття «Реальна майбутня вартість».
Реальна майбутня вартість - це вартість теперішніх грошових потоків через певний проміжок часу з урахуванням певної ставки відсотка і за відрахуванням суми коштів, які знеціняться під впливом інфляції.
Різниця між майбутньою вартістю та реальною майбутньою вартістю показує, яку суму знецінено під впливом інфляції.
Якщо інвестор закладав у номінальну процентну ставку інфляційну премію, то реальну майбутню вартість можна представити як різницю між майбутньою вартістю і інфляційною премією у вартісному виразі.
Реальну майбутню вартість можна визначити за наступною формулою.
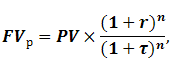(5.26)
де FVр – це реальна майбутня вартість;
PV – теперішня вартість;
r – номінальна дохідність у коефіцієнтній формі;
τ – темп інфляції в економіці у коефіцієнтній формі.
