Определение 30.1. Системой линейных дифференциальных уравнений 2-го порядка с постоянными коэффициентами называется система вида
Если правые части 
и 
тождественно равны 0, то система называется однородной, в противном случае ‑ неоднородной. Решением системы будем называть две функци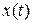и 
и 
, которые при подстановке в систему обращают ее уравнения в тождества. Решение системы иногда удобно записывать в виде вектор столбца
.
В дальнейшем будем рассматривать только линейные однородные системы. Рассмотрим 1-й метод решения (метод исключения, сводящий систему к линейному однородному дифференциальному уравнению с постоянными коэффициентами).
Продифференцируем 1-е уравнение системы:
и подставим сюда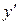 
из второго уравнения
.
Теперь исключим y с помощью первого уравнения, тогда получим
или
.
Таким образом, получили уравнение второго порядка. Его характеристическое уравнение
.
Зная корни характеристического уравнения, находим Ф.С.Р. 
, а затем получим
.
Пример 30.3. 
Составим характеристическое уравнение
.
отсюда
.
Общее решение
, 
,
или
.
Конец примера.
Рассмотрим второй метод решения, будем искать решение ввиде
.
Подставим в систему, получим
Отсюда, сокращая на 
и группируя, получим
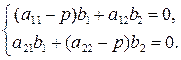
Эта система имеет не нулевые решения 
, если ее главный определитель отличен от нуля
.
Это уравнение называется характеристическим. Раскрывая, получим
.
Пусть его дискриминант 
(мы ограничемся только этим случаем), тогда имеются два вещественных корня 
и 
, которым соответствуют два решения
,
где 
‑ решения системы (1) при 
, 
‑ решения системы при 
. Общее решение системы этих уравнений будет
.
Список литературы
Основная литература:
1. Пискунов Н.С. Дифференциальное и интегральное исчисление для ВТУЗов. Т.1. ‑ М.: Интеграл-Пресс, 2004. – 416 с.
2. Пискунов Н.С. Дифференциальное и интегральное исчисление для ВТУЗов. Т.2. ‑ М.: Интеграл-Пресс, 2004. – 544 с.
3. Шипачев В.С., Высшая математика. Учеб. для вузов. ‑ 7-е изд., стер. - М.: Высшая школа. 2005. – 479 с.
4. Шипачев В.С. Курс высшей математики: Учеб. для вузов. ‑ 2-е изд., перераб. и доп. - М.: Проспект, 2005. ‑ 600 с.
5. Владимирский Б.К., Горстко А.Б., Ерусалимский Я.М. Математика. Общий курс. – СПб.: Издательство Лань, 2002. – 960 с.
6. Мантуров О.В., Матвеев Н.М., Курс высшей математики: Линейная алгебра. Аналитическая геометрия. Дифференциальное исчисление. - М.: Высш. шк., 1986. – 480 с.
7. Шестаков А.А., Малышева И.А., Полозков Д.П. Курс высшей математики: Интегральное исчисление. Дифференциальные уравнения. Векторный анализ./ Под ред. А.А. Шестакова. - М.: Высш. шк., 1987. – 320 с.
8. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 2: Дифференциальное и интегральное исчисление. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2004. ‑ 509 с.
9. Бугров Я. С., Никольский С. М. Сборник задач по высшей математике: Учеб. пособие для инж.-техн.спец.вузов / - 3-е изд., доп. - Ростов н/Д: Феникс, 1997. - 351с.
10. Бугров Я.С., Никольский С.М. Высшая математика: В 3-х т.; Учеб. для вузов инж.-техн. спец. Т. 3: Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. ‑ 6-е изд., стер. ‑ М.: Дрофа, 2004. ‑ 511 с.
11. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.1: Учеб. пособие для втузов.-5-е изд., испр.- М.:Высшая школа, 1997. – 304 с.
12. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2-х ч. Ч.2: Учеб. пособие для втузов.-5-е изд., испр.- М.:Высшая школа, 1997. – 416 с.
13. Сборник задач по математике для ВТУЗов т.1. Линейная алгебра и основы математического анализа / ред. А.В.Ефимов, Б.П.Демидович - М.:Наука, 1981. ‑ 464 с.
14. Сборник задач по математике для ВТУЗов. т.2. Специальные разделы математического анализа / ред., А.В.Ефимов, Б.П.Демидович. - М.: Наука, 1981. ‑ 367 с.
15. Сборник задач по математике для втузов. В 4 частях Ч. 1: Учеб. пособие для втузов /А.В. Ефимов, Ф.Ф. Каракулин, И.Б. Кожухов, А.С. Поспелов, А.А. Прокофьев. Под ред. А.В. Ефимова, А.С.Поспелова. ‑ 4-е изд. перераб. и доп. ‑ М.: Физ.-матем. лит., 2003. ‑ 288 с.
16. Сборник задач по математике для втузов: В 4 частях Ч. 2: Учеб. пособие для втузов /А.В. Ефимов, Ф.Ф. Каракулин, С.М. Коган, А.С. Поспелов, Р.Я. Шостак. Под ред. А.В.Ефимова, А.С.Поспелова. ‑ 4-е изд. перераб. и доп. ‑ М.: Физ.-матем. лит., 2003. ‑ 432 с.
17. Шипачев В.С. Задачник по высшей математике: Учеб. пособие для вузов. ‑ 4-е изд., стер. ‑ М.: Высш. школа, 2004. ‑ 304с.
18. Плис А.И., Сливина Н.А. Mathcad: Математический практикум для экономистов и инженеров: Учебное пособие. -М.: Финансы и статистика, 1999. – 656 с.
Дополнительная литература:
19. Никольский С. М. Курс математического анализа: Учеб. для физ. и мех.-мат. спец. вузов. Т.1. – 4‑е изд., перераб. и доп. ‑ М.: Наука, 1990. – 528 с.
20. Никольский С. М. Курс математического анализа: Учеб. для физ. и мех.-мат. спец. вузов. Т.2. ‑ 4-е изд., перераб. и доп. ‑ М.: Наука, 1991. – 543 с.
21. Ильин В.А., Поздняк Э.Г. Основы математического анализа. 4-е издание - М.: Наука, Гл. редакция физико-математической литературы, Ч.1, 1980. ‑ 616 с.
22. Ильин В.А., Поздняк Э.Г. Основы математического анализа. 4-е издание - М.: Наука, Гл. редакция физико-математической литературы, Ч.2, 1982. ‑ 448 с.
23. Карташев А.П., Рождественский Б.Л. Математический анализ. - М.: Наука, Гл. редакция физико-математической литературы, 1984. ‑ 448 с.
24. Фихтенгольц Г.М. Основы математического анализа. В 2-х томах. Т.1. – СПб.: Издательство «Лань», 2001. – 448 с.
25. Фихтенгольц Г.М. Основы математического анализа. В 2-х томах. Т.2. – СПб.: Издательство «Лань», 2001. – 464 с.
26. Краснов М.Л. Обыкновенные дифференциальные уравнения: Учеб. пособие для втузов. ‑ М.: Высш.шк., 1983. ‑ 128с.
27. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. Изд. 5-е. - М.: Наука, Гл. редакция физико-математической литературы, 1982. ‑ 332 с.
28. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. М.: Наука, Гл. редакция физико-математической литературы, 1980. – 232 с.
29. Федорюк М.В. Обыкновенные дифференциальные уравнения. - 2-е изд., перераб. и доп. - М.: Наука, Гл. редакция физико-математической литературы, 1985. ‑ 448 с.
30. Карташев А.П., Рождественский Б.Л. Обыкновенные дифференциальные уравнения и основы вариационного исчисления. 3‑е изд., перераб. и доп. ‑ М.: Наука, Гл. редакция физико-математической литературы, 1986. ‑ 272 с.
31. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. Учеб. пособие. - 2-е изд., перераб. - М.: Высш. шк., 1989. – 384 с.
32. Выполнение контрольных работ по теме «Интегральное исчисление». Методические указания к выполнению контрольных работ для студентов первого курса всех форм обучения всех специальностей /Кубан. гос. технолог. ун-т. А.В. Братчиков, И.В. Терещенко. Краснодар, 1994. ‑ 18с.
33. Дифференциальные уравнения. Методические указания по выполнению индивидуальных заданий для самостоятельной работы студентов 1 курса дневной формы обучения технологических специальностей /Кубан. гос. технолог. ун-т. Сост.: В.Г. Линенко, А.Л. Луцко, Ю.И. Коновалов, Н.В. Широкорядова. Краснодар, 1997. – 51 с.
34. Дифференциальные уравнения. Методические указания к типовым расчетным заданиям для студентов дневной и вечерней форм обучения 1 и 2 курсов всех специальностей. /Сост.: Н.И. Фомина, С.А. Свободина, Л.Г. Роганская ‑ Краснодар, изд. КПИ, 1988. ‑ 30с.
35. Функции многих переменных. Методические указания по выполнению индивидуальных заданий для самостоятельной работы студентов 1 курса дневной формы обучения технологических специальностей /Кубан. гос. технолог. ун-т. Сост.: В.Г. Линенко, А.Л. Луцко, Ю.И. Коновалов, Н.В. Широкорядова. Краснодар, 1997. – 51 с.
36. Дифференциальное исчисление функций нескольких переменных. Методические указания по выполнению индивидуальных заданий для самостоятельной работы студентов первого курса дневной формы обучения технологических специальностей /Кубан. гос. технолог. ун-т. Сост.: В.Г. Линенко, А.Л. Анкудинов, Н.А. Луцко, Б.Д. Семенов ‑ Краснодар, 1994. – 36 с.
37. Дифференциальное исчисление функций нескольких переменных. Методические указания по выполнению индивидуальных заданий для самостоятельной работы студентов первого курса дневной формы обучения технологических специальностей /Краснодар. политехн. ин-т. Сост.: В.Г. Линенко, А.Л. Анкудинов, Л.И. Ушакова, С.Я. Насибова ‑ Краснодар, 1991. – 52 с.
38. Неопределенный интеграл. Методическая разработка типовых расчетных заданий для студентов 1 курса дневной формы обучения технологических специальностей /Кубан. гос. технолог. ун-т. Сост.: Л.И. Ушакова, С.М. Михеева, И.В. Терещенко – Краснодар, 1998. – 45 с.
39. Непосредственное интегрирование. Методические указания по выполнению индивидуальных заданий для самостоятельной работы студентов первого курса дневной формы обучения технологических специальностей /Краснодар. политехн. ин-т. Сост.: С.Я. Насибова, Л.И. Ушакова, С.М. Михеева ‑ Краснодар, 1989. – 41 с.
40. Высшая математика: Методические указания и контрольные задания (с программой) для студентов-заочников инженерно-технических специальностей высших учебных заведений /Арутюнов Ю.С., Полозков А.П., Полозков Д.П. ‑ М.: Высш. школа, 1985. – 144 с.
