Определение 20.1. Обыкновенным дифференциальным уравнением n -го порядка называется уравнение вида:
,
которое содержит независимое переменное x, неизвестную функцию y (x), и ее производные вплоть до n -го порядка включительно.
Дифференциальное уравнение разрешено относительно производной n -го порядка, если его можно представить в виде
.
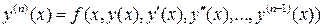Определение 20.2. Решением обыкновенного дифференциального уравнения n -го порядка называется всякая функция y (x), которая обращает его в тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием.
Определение 20.3. Множество решений обыкновенного дифференциального уравнения n -го порядка вида
,
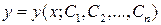где 
‑ произвольные постоянные, называется общим решением.
Каждый выбор этих постоянных дает частное решение. График частного решения называется интегральной кривой, а множество всех интегральных кривых называется семейством интегральных кривых.
Часто обыкновенное дифференциальное уравнение n‑ го порядка можно свести к уравнению вида
,
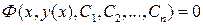где ‑ произвольные постоянные.
Оно называется общим интегралом. Каждый выбор этих постоянных дает частный интеграл 
.
Определение 20.4. Пусть дано обыкновенное дифференциальное уравнение n -го порядка и требуется найти его решение, удовлетворяющее начальным условиям
,
тогда говорят, что задана задача Коши:
,
.
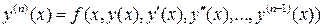Для обыкновенного дифференциального уравнения 1-го порядка сформулируем теорему существования и единственности решения задачи Коши:
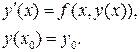
Теорема 20.1. Пусть функция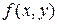 
непрерывна в замкнутой области D переменных 
, содержащей точку 
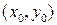, тогда, если частная производная этой функции по y непрерывна на этом множестве, то задача Коши на некотором отрезке 
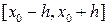имеет решение и это решение единственное.
Пример 20.1. Задача Коши
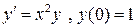
имеет единственное решение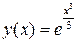 
, так как в любой замкнутой области, содержащей точку (0,1) функция 
и ее частная производная по y
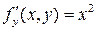
непрерывны.
Пример 20.2. Задача Коши
.
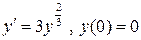имеет два решения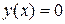 
и 
. Правая часть уравнения 
непрерывна в любой окрестности точки (0,0), но производная по y
терпит разрыв в точке (0,0). Поэтому условия применимости теоремы 1 нарушены. Возможность существования нескольких решений задачи Коши определяется теоремой Пеано.
Теорема 20.2. (Пеано) Если 
непрерывна на замкнутой области D переменных x, y, то при условии, что точка 
принадлежит этой области, задача Коши имеет хотя бы одно решение в некоторой окрестности точки 
.
ЛЕКЦИЯ № 21. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
