Рассмотрим уравнение
 .
.
Его общее решение имеет вид  , где
, где  - частное решение неоднородного дифференциального уравнения, а
- частное решение неоднородного дифференциального уравнения, а  - общее решение однородного дифференциального уравнения. Метод нахождения решения рассмотрен в лекции № 28. Для этого нужно найти фундаментальную систему решений. Зная ее можно методом вариации постоянных найти и частное решение линейного неоднородного уравнения. Если правая часть уравнения имеет специальный вид, то частное решение можно найти без использования метода вариации постоянных. Рассмотрим два важных случая.
- общее решение однородного дифференциального уравнения. Метод нахождения решения рассмотрен в лекции № 28. Для этого нужно найти фундаментальную систему решений. Зная ее можно методом вариации постоянных найти и частное решение линейного неоднородного уравнения. Если правая часть уравнения имеет специальный вид, то частное решение можно найти без использования метода вариации постоянных. Рассмотрим два важных случая.
1-Й СЛУЧАЙ
 ,
,
где a ‑ константа,  ‑ многочлен n -й степени. Если a не корень характеристического многочлена, то частное решение нужно искать в виде
‑ многочлен n -й степени. Если a не корень характеристического многочлена, то частное решение нужно искать в виде
 ,
,
где  - многочлен n -й степени с неопределенными коэффициентами. Его коэффициенты определяются после подстановки в уравнение методом неопределенных коэффициентов.
- многочлен n -й степени с неопределенными коэффициентами. Его коэффициенты определяются после подстановки в уравнение методом неопределенных коэффициентов.
Если a корень характеристического уравнения кратности r, то частное решение нужно искать в виде
 .
.
Рассмотрим случай, когда a = 0. Тогда  , поэтому частное решение имеет вид
, поэтому частное решение имеет вид
 ,
,
если 0 не корень характеристического уравнения и
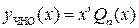 ,
,
если 0 корень характеристического уравнения кратности r.
Пример 29.1. Решить уравнение  .
.
Составим характеристическое уравнение  , его корни равны
, его корни равны  ,
,  .
.
В правой части стоит многочлен нулевой степени, поэтому  и частное решение будем искать в виде
и частное решение будем искать в виде
 .
.
Отсюда  , подставляя в уравнение, получим
, подставляя в уравнение, получим  . Тогда
. Тогда  и общее решение равно
и общее решение равно  .
.
Конец примера.
Пример 29.2. Решить уравнение  .
.
Характеристическое уравнение здесь такое же, как и в примере 29.1. В правой части находится многочлен первой степени, поэтому  . Следовательно, частное решение уравнения имеет вид
. Следовательно, частное решение уравнения имеет вид
 .
.
Вычислим производные
 ,
,
и подставим их в уравнение, тогда получим
 ,
,
или
 .
.
Отсюда
 ,
,
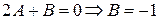 .
.
Отсюда  , а общее решение есть
, а общее решение есть
 .
.
Конец примера.
Пример 29.3. Решить уравнение  .
.
Составим характеристическое уравнение 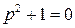 , его корни равны
, его корни равны  ,
,  .
.
В правой части стоит многочлен первой степени, умноженный на  , поэтому
, поэтому  и частное решение будем искать в виде
и частное решение будем искать в виде
 .
.
Вычислим производные

Отсюда, подставляя в уравнение, получим
 .
.
После сокращения на  , получаем соотношение
, получаем соотношение
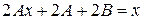 .
.
Отсюда
 ,
,
или
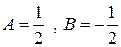 ,
,
то есть
 ,
,
а общее решение есть
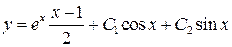 .
.
Конец примера.
2-Й СЛУЧАЙ

Здесь a и b числа, 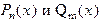 - многочлены n -й и m -й степени. Если комплексное число a+ib не является корнем характеристического уравнения, то частное решение ищут в виде
- многочлены n -й и m -й степени. Если комплексное число a+ib не является корнем характеристического уравнения, то частное решение ищут в виде
 ,
,
где N=max(n,m) - максимальное из чисел n,m  - многочлены степени N с неопределенными коэффициентами, которые нужно найти, подставляя
- многочлены степени N с неопределенными коэффициентами, которые нужно найти, подставляя  в уравнение.
в уравнение.
Если комплексное число a+ib является корнем характеристического уравнения кратности r (для квадратного уравнения кратность комплексного корня может быть равной только 1), то частное решение нужно искать в виде
 .
.
Рассмотрим случай, когда a = 0. Тогда 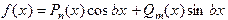 , поэтомучастное решение имеет вид
, поэтомучастное решение имеет вид
 ,
,
если ib не корень характеристического уравнения и
 ,
,
если ib корень характеристического уравнения кратности r.
Пример 29.4. Решить уравнение  .
.
Корни характеристического уравнения  и
и  . Число a+ib = 1+i не является корнем характеристического уравнения,
. Число a+ib = 1+i не является корнем характеристического уравнения,  , поэтому частное решение ищем в виде
, поэтому частное решение ищем в виде

Вычислим производные
 Подставляя в уравнение, получим
Подставляя в уравнение, получим

Сокращая на  и приводя подобные, получим
и приводя подобные, получим

Приравнивая коэффициенты при cos x и sin x, получим

Отсюда получаем 
А общее решение  .
.
КОНЕЦ ПРИМЕРА.
ПРИМЕР 5. Решить уравнение  .
.
Характеристическое уравнение  имеет корни
имеет корни  , число
, число  есть корень характеристического уравнения кратности r = 1, поэтому частное решение ищем в виде
есть корень характеристического уравнения кратности r = 1, поэтому частное решение ищем в виде

Вычисляя производные найдем
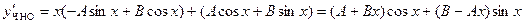

и подставляя в уравнение, получим
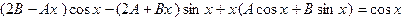
или

Отсюда  .
.
Тогда  , а общее решение
, а общее решение
 .
.
Конец примера.




