Определение 21.1. Дифференциальное уравнение

называется уравнением с разделяющимися переменными.
Теорема 21.1. Если  и существуют первообразные для функций
и существуют первообразные для функций 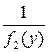 и
и  , то
, то  есть решение уравнения
есть решение уравнения  тогда и только тогда, когда
тогда и только тогда, когда  удовлетворяет соотношению
удовлетворяет соотношению
 .
.
Доказательство. Пусть  есть решение уравнения
есть решение уравнения  .
.
Тогда
 .
.
Интегрируя последнее соотношение, получим
 .
.
Пусть теперь  удовлетворяет равенству
удовлетворяет равенству
 .
.
Так как  , то, дифференцируя его по x, получим
, то, дифференцируя его по x, получим
 .
.
Конец доказательства.
Замечание 21.1.
 .
.
Это уравнение есть не что иное, как общий интеграл
 .
.
Замечание 21.2. Если  при
при  , то
, то  есть решение
есть решение  , оно может не удовлетворять общему интегралу и его необходимо учитывать отдельно.
, оно может не удовлетворять общему интегралу и его необходимо учитывать отдельно.
Рассмотрим теперь уравнение вида
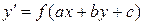 .
.
Покажем, что с помощью замены  это уравнение приводится к уравнению с разделяющимися переменными:
это уравнение приводится к уравнению с разделяющимися переменными:
 .
.
 ‑ уравнение с разделяющимися переменными. Разделяя переменные, получим
‑ уравнение с разделяющимися переменными. Разделяя переменные, получим
 .
.
Пример 21.1. Решить задачу Коши  .
.
Разделяя переменные, получим

При значении  получаем
получаем  ‑ решение уравнения, то есть общее решение уравнения есть
‑ решение уравнения, то есть общее решение уравнения есть
 .
.
Из начального условия получим
 .
.
Конец примера.
Пример 21.2. Найти общее решение уравнения 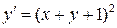 .
.
Выполним замену переменных  , тогда получим
, тогда получим  или
или  . Разделяя переменные, получим
. Разделяя переменные, получим
 .
.
Отсюда получаем  или
или  .
.
Конец примера.
Вопрос 21.2. Однородные дифференциальные уравнения первого порядка.
Определение 21.2. Дифференциальное уравнение вида  называется однородным дифференциальным уравнением.
называется однородным дифференциальным уравнением.
Покажем, что однородное дифференциальное уравнение подстановкой 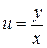 сводится к уравнению с разделяющимися переменными. Действительно
сводится к уравнению с разделяющимися переменными. Действительно  , тогда
, тогда 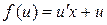 или
или
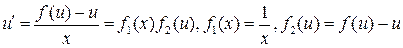 ,
,
то есть переменные разделились.
Пример 21.3. Решить уравнение  .
.
Подстановкой  получим
получим  или
или 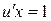 .
.
Разделяя переменные, найдем
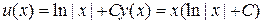 .
.
Конец примера.
Рассмотрим теперь уравнения вида
 .
.
Покажем, что подстановкой  уравнение сводится к однородному уравнению. Считаем, что
уравнение сводится к однородному уравнению. Считаем, что  , тогда
, тогда  . Теперь получаем
. Теперь получаем
 .
.
Выберем n и m так, чтобы

Эта система уравнений всегда имеет единственное решение, если главный определитель отличен от нуля
 .
.
Пусть n и m удовлетворяют этой системе, тогда получим
 ,
,
однородное дифференциальное уравнение.
Пример 21.3. Решить уравнение  .
.
 , тогда положим
, тогда положим  , причем n и m удовлетворяют системе уравнений
, причем n и m удовлетворяют системе уравнений
 ,
,
тогда  и
и  .
.
Выполнив замену  и подставив в уравнение, получим
и подставив в уравнение, получим
 или
или  .
.
Разделяя переменные, найдем
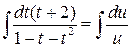 .
.
Пусть  , тогда получим
, тогда получим
 .
.
Интегрируя почленно, получим
 .
.
Подставляя  , получим
, получим
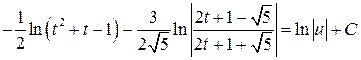 ,
,
где
 .
.
ЛЕКЦИЯ № 22. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.






