Определение 22.3. Дифференциальное уравнение
называется уравнением в полных дифференциалах, если существует такая функция 
, что
.
Из определения следует, что 
.
Так как 
, то 
‑ это условие, как можно показать, является необходимым и достаточным условием существования функции .
Из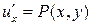 
при фиксированном y, получаем
.
Подставляя в 
, получаем
или
.
Так как 
, то функция 
зависит только от y: 
. Отсюда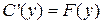 
. Решая это уравнение, найдем 
, тогда
,
Но 
, тогда получаем полный интеграл, из которого находим 
.
Пример 22.4. 
, это уравнение в полных дифференциалах, так как
.
Интегрируя при фиксированном y, получим
.
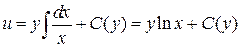Подставляя в 
, получим
.
Следовательно, 
.
Конец примера.
ЛЕКЦИЯ № 23. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
Вопрос 23.1. Уравнения вида.
Пусть 
есть решение уравнения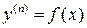 
, тогда интегрируя, получим
,
где 
‑ одна из первообразных для 
.
Итак, удовлетворяет новому дифференциальному уравнению, порядок которого на единицу ниже. Правая часть уравнения вновь есть функция только x, тогда интегрируя 2-й раз, получим:
.
Повторяя это еще (n -2) раза получим
.
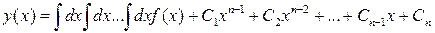‑ решение уравнения .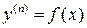
Пример 23.1. 
.
Конец примера.
Пример 23.2. Движение материальной точки под действием постоянной силы.
.
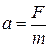‑ постоянное ускорение, поэтому 
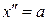, интегрируя, получим
,
, тогда
.
Вопрос 23.2. Уравнения вида.
Это уравнения, которые явно не содержат 
. Обозначим 
, тогда
,
то есть относительно 
получаем уравнение
,
порядок которого на k меньше исходного уравнения.
ПРИМЕР 23.3. 
.
Пусть 
, тогда 
и подставляя в уравнение, получаем 
‑ линейное неоднородное уравнение 1-го порядка. Решая его, найдем
или
Тогда, интегрируя дважды, получим
,
.
Конец примера.
Вопрос 23.3. Уравнение вида.
Это уравнение не содержит явно независимой переменной x и допускает понижение порядка подстановкой 
, тогда
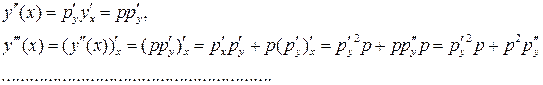
Каждый раз получаем выражение, которое имеет порядок производной на единицу ниже.
Пример 23.3. 
‑ уравнение математического маятника.
или разделяя переменные
.
Тогда 
, разделяя переменные, получим
.
Откуда
или
.
Конец примера.
Вопрос 23.4. Уравнения вида.
Это уравнение интегрированием сводится к уравнению (n -1) порядка
.
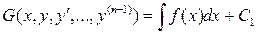Пример 23.4.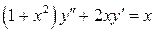 
.
, интегрируя правую и левую часть, получим
,
.
Конец примера.
Вопрос 23.5. Уравнения вида, где - однородная функция k-го порядка относительно.
По определению однородная функция k -го порядка удовлетворяет соотношению
.
Для таких уравнений делают подстановку 
. Тогда
,
и т.д. и сокращают уравнение на 
. Порядок уравнения понижается.
Пример 23.5. 
.
Подставляя 
, получим
или
.
Тогда
или после разделения переменных
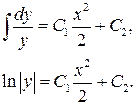
Отсюда, после переобозначения констант 
и 
.
Конец примера.
ЛЕКЦИЯ № 24. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.
