Очень часто необходимо искать производную неявной функции, причем в явном виде такую функцию представить удается редко. Оказывается, что можно найти выражение для производной неявной функции даже не зная ее явного вида.
Теорема 18.3. Пусть выполнены условия теоремы 18.1 и функция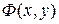 
непрерывна и дифференцируема на прямоугольнике 
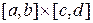. Причем 
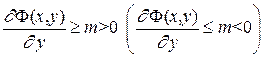, тогда уравнение 
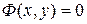определяет единственную неявную дифференцируемую функцию 
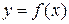с производной 
.
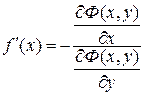Доказательство. Пусть для определенности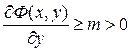 
, тогда для любого фиксированного x функция 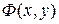монотонно возрастает по y. Из теоремы 18.2 следует, что в этом случае существует единственная неявная функция определяемая уравнением 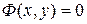. Обозначим ее через 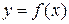. Докажем ее дифференцируемость. Рассмотрим разность
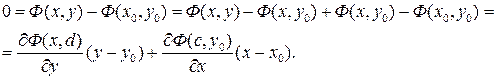
Здесь c и d лежат между значениями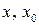 
и 
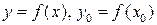. Отсюда получаем
.
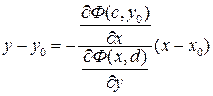Поделив на разнрсть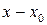 
, перейдем к пределу при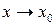 
.
Что и требовалось доказать.
Конец доказательства.
Пример 18.4. Как следует из примера 18.3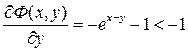 
и это дифференцируемая функция, поэтому неявная функция тоже дифференцируема и
,
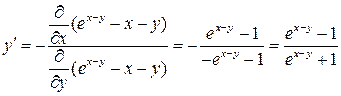для тех x и y, для которых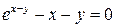 
.
Конец примера.
Теорема 18.4. Пусть функция 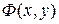непрерывна и дифференцируема в окрестности точк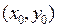и 
и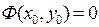 
. Если в этой окрестности частная производная 
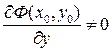и непрерывна, то существует некоторый интервал, содержащий точку 
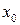, на котором определена единственная дифференцируемая неявная функция 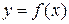, такая, что 
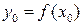и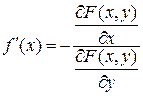 
.
Доказательство. Пусть для определенности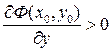 
. Тогда на некотором прямоугольнике 
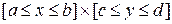, содержащем точку 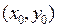, выполняется неравенство 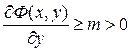в силу непрерывности производной. Следовательно, по y функция 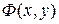монотонно возрастает при фиксированном значении 
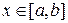. Отсюда следует, что на отрезке 
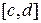функция 
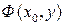принимает на концах этого отрезка разные знаки 
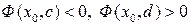. И, следовательно, в силу непрерывности функции 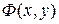на некотором отрезке 
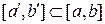эта функция принимает значения разных знаков 
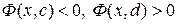. Теперь выполнены все условия теоремы 18.3, откуда следует справедливость теоремы 18.4.
Конец доказательства.
Пример 18.5. Пусть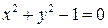 
, в точке 
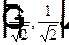частная производная 
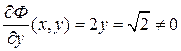, поэтому существует интервал, содержащий указанную точку, на котором определена единственная неявная функция 
.
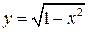Конец примера.
ЛЕКЦИЯ № 19. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ.
Вопрос 19.1. Условный экстремум.
Определение 19.1. Условным минимумом функции n переменных 
при наличии m условий связи
,
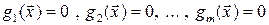называется точка 
, такая что
,
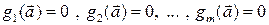и для всех 
из некоторой окрестности точки , удовлетворяющих уравнениям связи, выполняется неравенство 
.
Конец определения.
Определение 19.2. Условным максимумом функции n переменных при наличии m условий связи
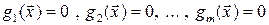
называется точка , такая что
,
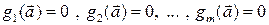и для всех из некоторой окрестности точки , удовлетворяющих уравнениям связи, выполняется неравенство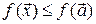 
.
Конец определения.
Определение 19.3. Условным экстремумом функции n переменных называется точка условного максимума или локального минимума.
Пример 19.1.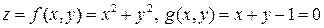 
.
Точкой условного минимума будет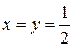 
(смотри рис. 1). Действительно из уравнения связи 
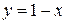, или 
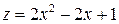, но 
.
Конец примера.
