Определение 17.1. Точка 
из множества M называется точкой локального минимума функции 
, если для любого 
из некоторой окрестности точки 
.
Определение 17.2. Точка из множества M называется точкой локального максимума функции , если для любого из некоторой окрестности точки 
.
Определение 17.3. Точка из множества M называется точкой локального экстремума функции , если она является точкой локального минимума или точкой локального максимума.
Пример 17.1.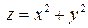 
. Точка (0,0) есть точка минимума, так как 
.
Конец примера.
Вопрос 17.2. Необходимое и достаточное условие существования локального экстремума функции нескольких переменных.
Теорема 17.1. Пусть имеет в точке локальный экстремум. Если функция дифференцируема в окрестности , то
.
Доказательство. Рассмотрим функцию 
. Эта функция одной переменной и она имеет в точке 
локальный экстремум. Так как 
существует, то 
, но тогда
.
Конец доказательства.
Пример 17.2. Функция 
имеет в точке (0,0) локальный экстремум и
,
и в точке локального экстремума
.
Конец примера.
Определение 17.4. Точки функции 
, в которых все ее частные производные 1-го порядка равны 0, называются стационарными.
Из теоремы 17.1 следует, что точки локального экстремума следует искать среди стационарных точек, однако не всякая стационарная точка есть точка локального экстремума, что следует из примера
Пример 17.3. 
.
Приравнивая произвдыне к 0, получим x =0 и y =0, но в стационарной точке (0,0) экстремума нет, так как в любой ее окрестности есть точки в которых 
или 
.
Конец примера.
Рассмотрим теперь достаточные условия существования экстремума функции нескольких переменных, ограничившись случаем функции двух переменных.
Теорема 17.2. (Достаточные условия существования локального экстремума). Пусть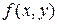 
имеет непрерывные производные вплоть до второго порядка включительно и пусть есть стационарная точка функции. Тогда
1) если 
‑ то - точка локального экстремума, причем
если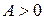 
, то ‑ точка локального минимума,
если 
, то ‑ точка локального максимума,
2) если 
‑ то не является точкой локального экстремума,
3) Если 
‑ то не является точкой локального экстремума.
где
.
Доказательство. Так как стационарная точка функции, то 
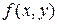. Тогда, разлагая в этой точке, получим
или
Введем разности 
. Тогда получим, с учетом того, что частные производные непрерывны
Введем обозначения
.
Тогда
Пусть 
, тогда выделяя полный квадрат, получим
или
Если величина 
, тогда разность 
сохраняет знак, то есть в точке 
существует локальный экстремум, причем если 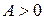, то в этой точке локальный минимум, если , то локальный максимум.
Пример 17.3. Пусть 
. Найдем стационарные точки функции
Решая систему, найдем 
и 
. То есть стационарной точкой является точка 
. Найдем вторые производные
.
и вычислим определитель
.
Тогда в точке ‑ локальный минимум.
Конец примера.
