Пусть L плоская кривая, начало и конец которой расположены в точках A и B. Разобьем кривую AB n +1 точкой 
. Соединим их отрезками прямых, тогда получим ломаную 
. Пусть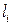 
‑ длина i -го звена ломаной. Положим 
. Тогда, если существует предел
,
то его называют длиной дуги AB, а саму кривую называют спрямляемой (см. рис. 1).
Рис. 1. Длина плоской кривой.
Определение 10.1. Пусть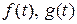 
две непрерывные функции на отрезке 
. Уравнения вида
называются параметрическими уравнениями плоской непрерывной кривой, переменную t ‑ называют параметром. Если 
и 
непрерывные функции, то кривая называется гладкой.
Теорема 10.1. Пусть L ‑ параметрически заданная гладкая кривая, тогда ее длина равна
.
Доказательство. Разобьем отрезок на части точками 
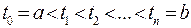. Пусть эти значения параметра соответствуют точкам кривой 
. Длина i -го звена ломаной равна
.
По теореме Лагранжа
,
.
Тогда
,
составив сумму длин всех звеньев ломаной, получим интегральную сумму
,
которая, в силу непрерывности производных при 
, сходится к интегралу
.
Конец доказательства.
Если кривая задана функций 
, нетрудно получить формулу длины гладкой кривой, если положить
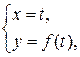
тогда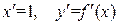 
, и, следовательно,
.
Пример 10.1. Вычислить длину параболы 
на отрезке 
.
={интегрируем по частям}= 
Решая уравнение, получим
.
Определение 10.2. Кривая называется замкнутой, если значениям параметра 
и 
соответствует одна и также точка кривой (см. рис. 2).
Определение 10.3. Если некоторому внутреннему значению параметра соответствуют две разные точки кривой, то кривая называется самопересекающейся (см. рис. 2).
Рис 2. Замкнутая и самопересекающая кривые.
Вопрос 10.2. Кривизна и радиус кривизны плоской кривой.
Пусть плоская кривая задана функцией , имеющей непрерывную вторую производную. Пусть длина дуги 
равна S, а ‑ угол между касательными в точках M и 
(см. рис. 2).
Рис. 3. Кривизна плоской кривой.
Определение 10.4. Кривизной плоской кривой в точке M называется предел
.
Величина обратная модулю кривизны называется радиусом кривизны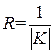 
.
Теорема 10.2. Если кривая задана дважды непрерывно дифференцируемой функцией , то ее кривизна равна
.
Доказательство. Пусть точке M соответствует аргумент x, а точке ‑ аргумент 
. Длина кривой S равна
,
где была использована теорема о среднем значении. Так как 
, то 
и поэтому, применяя формулу Лагранжа, получим
или
,
тогда
.
Конец доказательства.
Пример 10.2. Вычислить кривизну и радиус кривизны окружности 
.
.
Подставляя в формулу кривизны, получим
.
ЛЕКЦИЯ № 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
