Свойство 6.4. (Линейность определенного интеграла)
.
Доказательство. Используя линейность интегральной суммы и свойства предела, получим
.
Отсюда получаем доказываемое равенство.
Конец доказательства.
Следствие 6.3. Если функции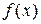 
и 
определены на отрезке 
, причем 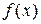интегрируема на отрезке , а функция и отличается от функции 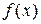в счетном числе точек, то функция интегрируема на отрезке и
.
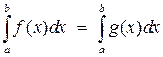Доказательство. Приведем доказательство для случая, когда число точек, в которых 
, конечно. Пусть это будут точки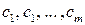 
отрезка . Рассмотрим функцию 
. Тогда 
только, если 
. Положим 
. Тогда выполнив произвольное разбиение отрезка с диаметром 
, и, учитывая, что каждая точка 
принадлежит не более чем двум отрезкам 
, получим для интегральной суммы функции 
неравенство:
.
Переходя в нем к пределу при 
, получим 
. В силу свойства линейности, функция 
интегрируема на отрезке и
.
Конец доказательства.
Из данного следствия вытекает важный вывод:
Следствие 6.4. Интеграл не изменится, если изменить у интегрируемой на отрезке функции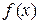 
значения не более чем в счетном числе точек.
Свойство 6.5. (Нормировка определенного интеграла). Если 
на отрезке , то 
.
Доказательство. Интегральные суммы единичной функции равны 
. Поэтому, вычисляя предел такой постоянной суммы, получим, что интеграл равен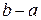 
.
Конец доказательства.
Свойство 6.6. (Положительная определенность определенного интеграла). Если 
, то 
.
Доказательство. Пусть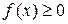 
, тогда по свойству положительности интегральных сумм 
. Переходя к пределу, получим, что интеграл неотрицателен.
Конец доказательства.
Следствие 6.5. Если 
, то 
.
Доказательство. Из неравенства следует, что 
, тогда
Конец доказательства.
Свойство 6.7. Если функци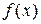и и интегрируемы на отрезке 
, то и их произведение 
интегрируемо на отрезке .
Приводится без доказательства.
Свойство 6.8. ( Теорема о среднем значении). Если 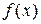непрерывна на , то найдется точка c из этого отрезка такая, что 
.
Доказательство. Пусть минимальное и максимальное значения функции 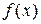на отрезке соответственно равны m и M. Интегрируя неравенство 
, получим
.
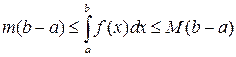или
.
В силу непрерывности функции найдется такая точка c отрезка , что
.
Конец доказательства.
Свойство 6.9. Если функция 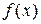интегрируема на отрезке , то ее модуль 
также интегрируем на отрезке , при чем справедливо неравенство
.
Доказательство. Первая часть теоремы, т.е. доказательство интегрируемости модуля функции приводится без доказательства. Из неравенства
Следует, что
,
или
.
Конец доказательства.
ЛЕКЦИЯ № 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
