Вопрос 6.1. Интегральная сумма и определенный интеграл Римана.
Пусть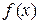 
задана на 
. Разобьем отрезок n +1 точкой 
на n отрезков 
. Будем обозначать это разбиение отрезка буквой Т. Пусть 
‑ произвольная точка из отрезка разбиения 
длины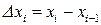 
.
Определение 6.1. Число 
, равное
называется интегральной суммой Римана функции 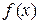, соответствующей разбиению T отрезка на части и выбору промежуточных точек на отрезках разбиения .
Конец определения.
Определение 6.2. Величина 
, то есть длина наибольшего из отрезков разбиения, называется диаметром разбиения T.
Конец определения.
Перечислим свойства интегральных сумм:
Свойство 6.1. (Нормировка интегральных сумм). Если 
на отрезке 
, то 
.
Доказательство.
.
Конец доказательства.
Свойство 6.2. (Положительная определенность интегральных сумм).
Если 
на отрезке , то 
.
Доказательство. Так как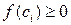 
и 
, то 
.
Конец доказательства.
Свойство 6.3. (Линейность интегральных сумм). Интегральная сумма от линейной комбинации функций 
есть линейная комбинация интегральных сумм этих функций.
.
Доказательство. 
. Раскрывая скобки и группируя слагаемые, получим
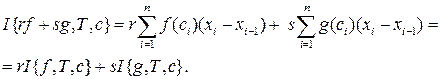
Конец доказательства.
Геометрический смысл интегральной суммы: интегральная сумма (см. рис. 1) 
функции 
на отрезке есть площадь ступенчатой фигуры, составленной из прямоугольников высотой 
и шириной 
.
Рис. 1. Геометрический смысл интегральной суммы.
Определение предела интегральных сумм функции 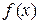на отрезке 
можно дать, например, на языке 
следующим образом.
Определение 6.3. Число I называется пределом интегральных сумм функции 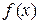на отрезке , если для любого сколь угодно малого положительного числа e существует такое положительное число 
, может быть зависящее от e, что для любого разбиения Т отрезка , диаметр которого удовлетворяет неравенству 
, независимо от способа разбиения отрезка на части и от выбора промежуточных точек выполняется неравенство 
.
Конец определения.
Предел интегральных сумм будем в дальнейшем обозначать символом
.
Из определения предела интегральных сумм, подобно пределу последовательности или функции, следует его единственность.
Теорема 6.1. (Единственность предела интегральных сумм). Если существует предел интегральных сумм функции 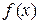на отрезке , то он единственен.
Доказательство. Предположим противное. Пусть для функции 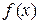на отрезке существует два различных значения предела интегральных сумм 
. Пусть выбрано 
. Тогда должно существовать такое число 
, что для разбиений с диаметром 
выполняются неравенства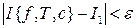 
и 
. Тогда
или
.
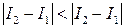Полученное противоречие доказывает теорему 6.1.
Конец доказательства.
Определение 6.4. Определенным интегралом от функции 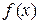на отрезке или интегралом Римана называется предел интегральных сумм при стремлении диаметра разбиения к нулю, обозначаемый символом
,
при условии, что величина предела не зависит от способа разбиения отрезка на части и выбора промежуточных точек . Функции, для которых существует на отрезке определенный интеграл, называются интегрируемыми (по Риману).
Конец определения.
