Определение 3.2. Простейшими рациональными дробями называются дроби вида:
,
причем квадратный трехчлен имеет только комплексные корни (отрицательный дискриминант 
).
Справедлива следующая теорема (без доказательства):
Теорема 3.7. Любая правильная рациональная дробь 
может быть разложена на сумму простейших рациональных дробей, при этом если знаменатель 
разложен на множители, то
множителю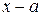 
соответствует одна дробь 
,
множителю 
соответствует сумма дробей 
, множителю 
соответствует дробь 
,
множителю 
соответствует сумма дробей
.
Рассмотрим метод нахождения неопределенных постоянных в разложении рациональной дроби на простейшие (метод неопределенных коэффициентов):
a) простые действительные корни (то есть их кратность равна единице), приведем их к общему знаменателю
.
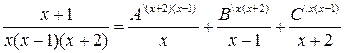и приравняем числители
.
Положим 
, т.е. корням знаменателя, тогда
то есть
.
b) кратные действительные корни или комплексные корни.
.
После приведения к общему знаменателю приравниваем числители
.
Положим 
, то есть корню знаменателя, тогда 
, тогда получим, перенеся слагаемое 
в левую часть равенства
или
,
подставив вновь , получим 
. Перенесем в левую часть слагаемое 
, найдем
,
или после сокращения на x +2
,
откуда найдем, 
. Следовательно,
.
Вопрос 3.4. Интегрирование простейших дробей.
Простейшие дроби первых двух типов сводятся к табличным простой заменой переменной:
1) 
.
2) 
.
Простейшие дроби третьего типа вычисляются путем выделения полного квадрата из квадратного трехчлена, стоящего в знаменателе и соответствующих замен переменных
3) 
,
где 
.
Формула получается следующим образом. Выделим полный квадрат в знаменателе
где 
(так как дискриминант ).
Введем замену переменных 
, тогда получим интеграл
Второй интеграл табличный 
. В первом сделаем замену 
, тогда получим
.
Откуда
.
отсюда получается доказываемая формула заменой 
.
4) 
,
где
‑ многочлен степени 
с неопределенными коэффициентами
C,D ‑ неизвестные коэффициенты.
Для определения коэффициентов нужно продифференцировать левую и правую часть равенства и применить метод неопределенных коэффициентов. Метод вычисления интеграла от рациональной дроби по этой формуле является частным случаем метода Остроградского.
Вопрос 3.5. Примеры интегрирования рациональных дробей.
Пример 3.6. 
.
Разложим дробь на простейшие
или
.
1-й способ (основной):
.
Приравняем коэффициенты при одинаковых степенях x
,
отсюда 
2-й способ:
Положим x равным корням знаменателя рациональной дроби, то есть положим
Отсюда получаем
.
Конец примера.
Пример 3.7.
.
Разложим дробь на простые
,
и приведем правую часть к общему знаменателю. Приравняем числители, тогда
.
1-й способ:
2-й способ:
.
Положим x равным корню знаменателя, то есть x =1, тогда получим 2=2 B или B =1. Подставляя это в равенство, получим
,
или
.
Откуда
.
Положим 
.
Положим 
.
Тогда получим
Откуда получим
Конец примера.
Пример 3.8. 
.
.
Приведем правую часть к общему знаменателю и приравняем числители
Найдем коэффициенты
1-й способ:
Раскроем скобки и сгруппируем слагаемые по степеням x
.
Приравнивая коэффициенты при одинаковых степенях x, получим:
Отсюда 
и получаем систему
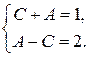
Решая ее, найдем 
.
2-й способ:
Положим x равным корню знаменателя, то есть x =1, тогда получим 
. подставляя 
в равенство, получим
или
или
.
Сокращая на общий множитель 
, найдем
,
откуда 
.
Отсюда получаем разложение
.
Отсюда получаем
Конец примера.
Пример 3.9. 
.
Для вычисления применим метод Остроградского
.
Дифференцируя это равенство, получим
.
Приведем правую часть к общему знаменателю
и приравняем числители
.
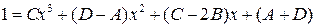Сравнивая коэффициенты при старших степенях, получим:
Отсюда находим 
. Поэтому получаем
Конец примера.
