Вопрос 4.1. Интегрирование дробно-линейных иррациональностей.
Определение 4.1. Многочленом двух переменных x и y называется функция вида
.
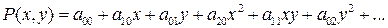Конец определения.
Пример 4.1. 
‑ многочлен второй степени двух переменных.
Конец примера.
Определение 4.2. Рациональной функцией двух переменных x и y называется отношение двух многочленов:
.
Конец определения.
Пример 4.2.
.
Конец примера.
Определение 4.3. Функция вида
.
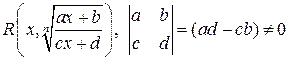называется дробно-линейной иррациональностью, где R рациональная дробь двух переменных.
Конец определения.
Аналогично определяются рациональные функции трех и более переменных.
a) Интеграл вида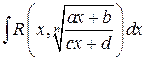 
вычисляется с помощью подстановки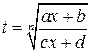 
.
Пример 4.3. Вычислить интеграл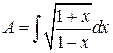 
.
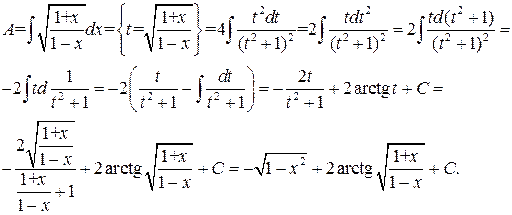
Конец примера.
б) Интеграл вида
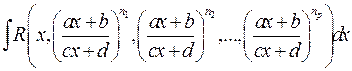
где 
, 
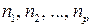рациональные числа, вычисляется с помощью подстановки 
, где r ‑ наименьший общий знаменатель дробей .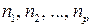
Пример 4.4.
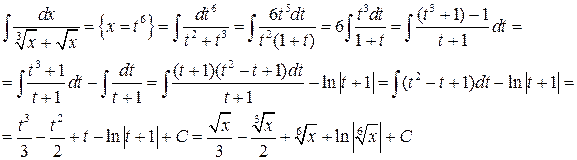
Конец примера.
Вопрос 4.2. Интегрирование квадратичных иррациональностей.
а) Интеграл вида 
выделением полного квадрата сводится к интегрированию табличных интегралов
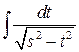или 
.
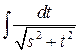Пример 4.5.
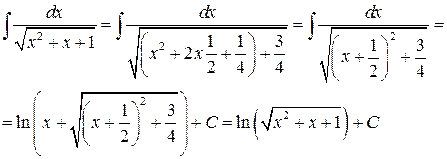
Конец примера.
б) Интеграл вида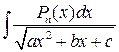 
вычисляется по методу неопределенных коэффициентов
,
где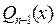 
‑ многочлен с неопределенными коэффициентами, - неопределенное число.
Пример 4.6.
.
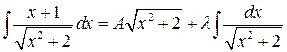Дифференцируя по x, получим
,
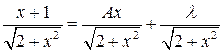или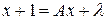 
, откуда A =1, =1, и, следовательно,
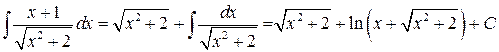
Конец примера.
в) Интеграл вида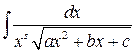 
вычисляется заменой 
.
Пример 4.7.
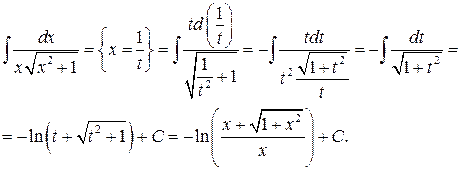
Конец примера.
ЛЕКЦИЯ № 5 НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Вопрос 5.1. Интегрирование тригонометрических выражений.
a) Интегралы вида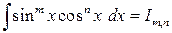 
.
1) если 
‑ нечетное натуральное число, n ‑ любое вещественное число, то
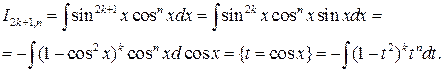
2) если 
‑ нечетное натуральное число, m ‑ любое вещественное число, то
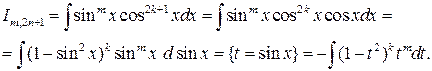
Пример 5.1.
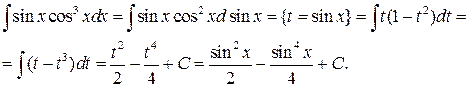
Конец примера.
3) 
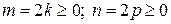‑ четные числа. Степени понижаются посредством перехода к двойному аргументу по формулам:
.
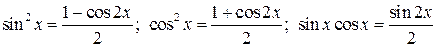Пример 5.2.
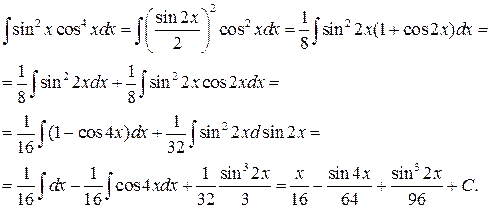
Конец примера.
4) Если 
, где k ‑ целое число, то делается подстановка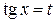 
или 
.
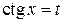Пример 5.3.
.
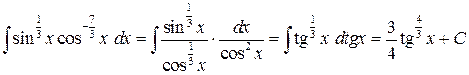Конец примера.
5) Если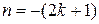 
‑ отрицательное нечетное число, n ‑ целое число, то делается подстановка 
.
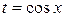Пример 5.4.
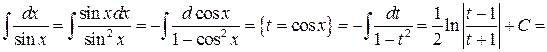
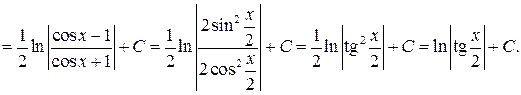
Конец примера.
6) Если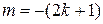 
‑ отрицательное нечетное число, m - целое число, то делается подстановка 
.
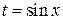Пример 5.5.
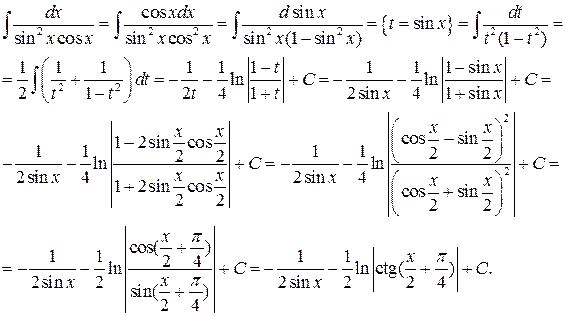
Конец примера.
b) Интегралы вида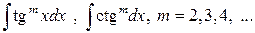 
Для вычисления интегралов используются тригонометрические формулы:
.
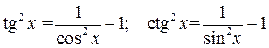Пример 5.6.
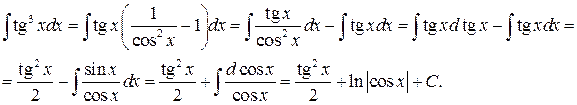
Конец примера.
с) Интегралы вида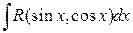 
, где 
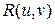‑ рациональная функция двух переменных u, v.
I) Универсальная тригонометрическая подстановка
,
,
.
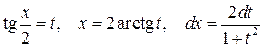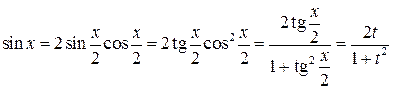Универсальная тригонометрическая подстановка сводит интеграл к интегралу от рациональной функции: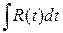 
.
Пример 5.7.
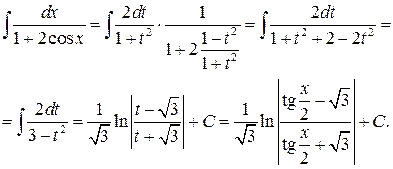
Конец примера.
II) Если выполнено равенство 
, то более подходит подстановка 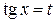. Тогда получаем
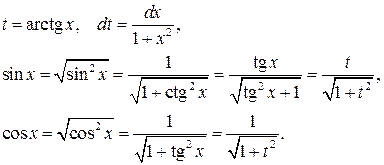
Эта подстановка сводит интеграл к интегралу от рациональной функции.
Пример 5.8.
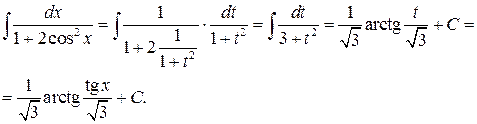
Конец примера.
