Определение 24.3. График функции 
имеет на интервале (a,b) выпуклость направленную вверх (вниз), если любая касательная, проведенная к графику функции на этом интервале, лежит выше (ниже) графика .
Замечание. Иногда используется такая терминология: вогнутый ‑ выпуклый вниз, выпуклый ‑ выпуклый вверх.
Теорема 24.4. (Достаточные условия выпуклости графика функции на интервале (a, b)). Пусть на интервале (a, b) 
(
), тогда график на интервале имеет выпуклость направленную вниз (вверх).
Доказательство. Пусть для определенности на (a,b). Тогда разложим по формуле Тейлора в окрестности произвольной точки c (a < c < b)
.
Обозначим 
. Это уравнение описывает касательную. Тогда получаем
или
.
Отсюда следует, что касательная расположена ниже графика . В силу произвольности точки c, заключаем, что график функции выпукл вниз.
Конец доказательства.
Определение 24.4. Точка a называется точкой перегиба графика функции , если при переходе через эту точку направление выпуклости меняется на противоположное. Так как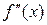 
меняет знак при переходе через точку перегиба a, то точка a есть точка локального экстремума функции , и мы получаем необходимые и достаточные условия существования точки перегиба.
Теорема 24.5. (Необходимые условия существования точки перегиба). Если a есть точка перегиба , то 
, или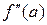 
не существует.
Определение 24.5. Точки функции , в которых вторая производная обращается в ноль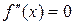 
или не существует, называются критическими точками 2-го рода.
Теорема 24.6. (Достаточные условия существования точки перегиба). Если при переходе через точку 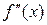меняет знак на противоположный, то эта точка есть точка перегиба, если знак второй производной не меняется, то это не точка перегиба.
Пример 24.4.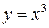 
. Находим критическую точку: 
, 
, 
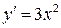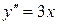при 
. При переходе через эту точку знак y'' меняется на противоположный.
Конец примера.
ЛЕКЦИЯ № 25. ИССЛЕДОВАНИЕ ФУНКЦИЙ.
Вопрос 25.1. Асимптоты графика функции.
Определение 25.1. Вертикальной асимптотой функции называется прямая линия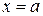 
, если один из пределов 
или 
равен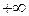 
или 
.
Из определения следует, что точка a есть точка разрыва второго рода и, следовательно, вертикальные асимптоты будут проходить через те точки на прямой x, которые лежат среди точек разрыва 2-го рода и в окрестности которых функция неограничена. Поэтому у элементарных функций наклонные асимптоты могут проходить только через те точки, в которых эти функции неопределенны. График функции не может пересекать вертикальную асимптоту.
Пример 25.1.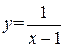 
, так как 
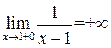или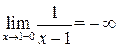 
, то прямая 
есть вертикальная асимптота.
Конец примера.
Определение 25.2. Прямая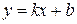 
называется наклонной асимптотой графика функции при 
, если 
.
Смысл этого определения: расстояние между графиком функции и асимптотой по вертикали стремится к нулю при 
или при 
. Наклонная асимптота может многократно пересекать график функции. Если коэффициент наклона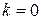 
, то асимптота называется горизонтальной.
Теорема 25.1. Для того, чтобы прямая 
была наклонной асимптотой графика функции при 
, необходимо и достаточно, чтобы существовали пределы:
,
.
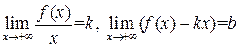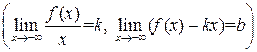. Доказательство. Рассмотрим только случай 
, так как в случае доказательство аналогично.
Необходимость: Пусть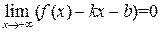 
, тогда
.
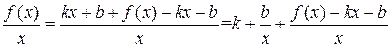Следовательно
.
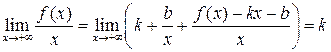и
.
Достаточность: Пусть 
и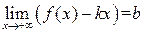 
. Тогда
.
Конец доказательства.
Пример 25.2. Найти асимптоты функции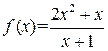 
.
Найдем наклонные асимптоты:
,
,
Следовательно, при стремлении функция имеет наклонную асимптоту 
. Так как значения k и b в вычисленных пределах не зависят от знака бесконечности, то при стремлении получаем туже наклонную асимптоту. График функции и ее асимптоты приведены на рис. 1.
Рис. 1. Асимптоты графика функции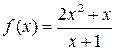 
.
