Вопрос 15.1. Подпоследовательности.
Определение 15.1. Пусть дана последовательность 
и возрастающая последовательность натуральных чисел
тогда последовательность 
называется подпоследовательностью последовательности .
Теорема 15.1. Если последовательность сходится, то сходится ее любая подпоследовательность, причем к тому же самому пределу.
Доказательство. Из сходимости последовательности следует, что для любого 
существует 
такое, что для всех 
выполняется неравенство 
, но тогда для всех 
.
Конец доказательства.
Пример 15.1. Пусть дана последовательность
Эта последовательность сходится
Выделим из нее подпоследовательность
Эта подпоследовательность, согласно теореме 15.1, должна сходится к нулю, что легко доказать непосредственно
.
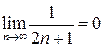Конец примера.
Лемма 15.1. (Принцип вложенных отрезков) Всякая бесконечная система вложенных отрезков содержит хотя бы одну общую точку.
Доказательство. Бесконечной системой вложенных отрезков называется система отрезков вида 
, где 
и 
монотонные последовательности, ограниченные сверху величиной 
, а снизу ‑ величиной 
. В силу этого существуют пределы:
,
причем для любого n справедливы неравенства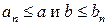 
.
Выбрав a, мы найдем искомую точку.
Конец доказательства.
Лемма 15.2. (Сравнительный признак сходимости) Пусть даны три вещественные последовательности, n -е члены которых связаны неравенствами 
. Если сходятся последовательности 
и 
то сходится и последовательность 
, причем 
Доказательство. Из условия леммы следует неравенство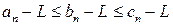 
. Тогда, из определения предела последовательности, следует, что для любого существует число , такое, что для всех справедливы неравенства
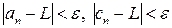
или
Тогда выполняется неравенство
Откуда
или
Конец доказательства.
Используем леммы 15.1 и 15.2 для доказательства теоремы 2.
Теорема 15.2. (Больцано ‑ Вейерштрасса) Всякая ограниченная последовательность содержит сходящуюся подпоследовательность.
Если последовательность ограничена, то все ее n -е члены удовлетворяют неравенству 
. Выберем любой член последовательности и разделим отрезок. Из двух полученных отрезков выберем тот, который содержит бесконечно много членов последовательности. Затем повторим процесс вновь и вновь, выбирая каждый раз перед делением отрезков произвольный член последовательности. В результате получим вложенную систему отрезков, длина которых стремится к нулю, и подпоследовательность, удовлетворяющую неравенствам
где 
‑ выделенная подпоследовательность.
Из доказательства леммы 15.1 следует существование пределов
.
Так как длина вложенных отрезков стремится к нулю
то 
, а из леммы 15.2 следует, что сходится и подпоследовательность 
Конец доказательства.
Определение 15.2. Числовая последовательность называется последовательностью Коши или фундаментальной, если для любого существует натуральное число такое, что для и любого натурального p справедливо неравенство 
для всех p =1,2,3,....
Теорема 15.3. Сходящаяся последовательность фундаментальна.
Доказательство. Если 
, то для любого существует такое, что для всех справедливо неравенство
.
Следовательно, для любого натурального p
откуда
Конец доказательства.
Теорема 15.4. (Критерий Коши) Если последовательность фундаментальна, то она сходится.
Доказательство. Доказательство теоремы проводится в два этапа. На первом этапе доказывается ограниченность фундаментальной последовательности. На втором этапе с помощью теоремы Больцано-Вейерштрасса устанавливается наличие сходящейся подпоследовательности и доказательство на этой основе сходимости самой последовательности.
