Вопрос 20.1. Производная n -го порядка.
Определение 20.1. Пусть дана функция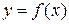 
. Производной n ‑го порядка от функции 
называется производная от производной 
‑го порядка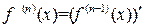 
.
Производная второго порядка обозначается
или 
или 
Производная третьего порядка обозначается
или 
или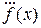 
Точками порядок производной принято указывать в теоретической механике. Производные более высоких порядков обозначают, указывая порядок или арабскими или римскими числами
, 
или 
.
Пример 20.1. Вычислить производную второго порядка от 
.
Конец примера.
Для производной n -го порядка справедливы формулы
1) 
,
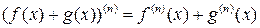2) 
,
3) 
,
4) формула Лейбница 
,
где
‑ биномиальные коэффициенты, 
.
Пример 20.2.
,
.
Конец прмера.
Вопрос 20.2. Дифференциал n -го порядка.
Определение 20.2. Дифференциалом n -го порядка называется произведение 
и обозначается
.
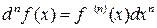Дифференциал n -го порядка обладает следующими свойствами:
1) 
2) 
3) 
4) 
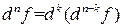
5) формула Лейбница 
,
где
‑ биномиальные коэффициенты, .
Доказательство. Свойства 1) ‑ 3) и 5) есть следствия соответствующих свойств n -й производной. Докажем теперь 4‑е свойство. Пусть x ‑ независимая переменная. Тогда
.
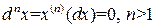Далее, так как 
, то 
, и, следовательно, 
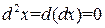, поэтому 
. Тогда последовательно получаем
,
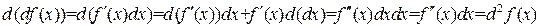то есть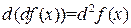 
. Аналогично
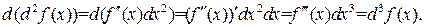
Продолжая, получим
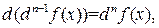
откуда следует
Пример 20.3. Вычислить 
от 
.
Конец примера.
Вопрос 20.3. Теорема Ферма и Ролля.
Определение 20.2. Точка a называется точкой локального минимума функции , если существует окрестность точки a, такая, что для всех x из этой окрестности справедливо неравенство 
Определение 20.3. Точка a называется точкой локального максимума функции , если существует окрестность точки a, такая, что для всех x из этой окрестности справедливо неравенство 
.
Определение 20.4. Точка а называется точкой локального экстремума функции , если она является или точкой локального минимума, или точкой локального максимума.
Теорема 20.2. (Ферма). Если в точке a имеет локальный экстремум и дифференцируема в этой точке, то (см. рис. 1) 
.
Доказательство. Пусть a есть точка локального минимума. Тогда для достаточно малых h 
. Односторонние производные в точке a равны
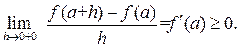
Отсюда следует равенство 
.
Конец доказательства.
Теорема 20.3. (Ролля). Пусть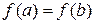 
и функция непрерывна на отрезке [ a,b ] и дифференцируема на интервале (a,b). Тогда обязательно найдется точка c, такая, что a<c<b и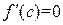 
.
Рис. 1. К доказательству теорем Ферма и Ролля.
Доказательство. Из непрерывности функции на отрезке 
следует существование точек 
и 
этого отрезка, в которых функция принимает максимальное и минимальное значения M и m (пусть для определенности 
и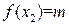 
). Если M=m, то 
и 
для всех x из отрезка . Для этого случая теорема доказана. Если 
, то или 
, или 
. Тогда внутри отрезка 
существует точка локального экстремума c, в которой по теореме Ферма .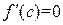
Конец доказательства.
Теорема 20.4 (Коши). Пусть функции и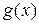 
непрерывны на отрезке [ a,b ] и дифференцируемы внутри этого отрезка. Тогда существует точка c такая, что a<c<b и
Доказательство. Введем вспомогательную функцию
,
тогда
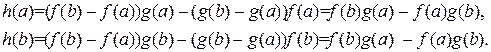
То есть 
. Применяя к функции 
теорему Ролля (проверьте условия ее применимости), получим
.
Откуда
или
Конец доказательства.
