Общее определение функции определяет последнюю как закон соответствия между множествами X и Y. Если X и Y ‑ числовые множества, то мы получаем числовую функцию одного аргумента.
Функции можно разбить на четыре следующих класса:
1) вещественные функции вещественного аргумента,
2) комплексные функции вещественного аргумента,
3) вещественные функции комплексного аргумента,
4) комплексные функции комплексного аргумента.
Любую функцию второго типа можно представить в виде 
, где 
и 
‑ вещественные функции.
В дальнейшем будем рассматривать только функции первого типа.
Определение 16.1. Графиком функции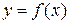 
называется геометрическое место точек плоскости с координатами.
В некоторых случаях график функции может быть построен путем простых преобразований графика известной функции 
:
а) график функции 
получается сдвигом вдоль оси X на a единиц влево, если 
, и на a единиц вправо, если 
, графика ;
б) график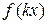 
получается растяжением в k раз, если 
, и сжатием в k раз, если 
, графика функции вдоль оси X;
в) график 
получается растяжением в A раз, если 
, и сжатием в A раз, если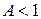 
, графика функции вдоль оси Y;
г) график 
получается путем последовательного применения преобразований а) ‑ в) с учетом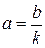 
.
Существует три основных способа задания функции:
1) аналитический (задание формулой),
2) графический,
3) табличный (задание таблицы y и x).
Определение 16.2. Функция 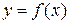называется
а) монотонно возрастающей, если для всех 
выполняется неравенство 
,
б) монотонно убывающей, если для всех выполняется неравенство 
,
в) монотонно невозрастающей, если для всех выполняется неравенство 
,
г) монотонно неубывающей, если для всех выполняется неравенство 
.
Определение 16.3. Функция называется четной, если для всех x из области определения, 
.
Определение 16.4. Функция называется нечетной, если для всех x из области определения, 
.
Определение 16.5. Функция называется периодической, если существует число 
такое, что 
.
Определение 16.6. Функция 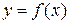называется взаимно однозначной, если для любых 
выполняется неравенство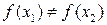 
.
Примеры таких функций: 
.
Легко видеть, что любая монотонно возрастающая или монотонно убывающая функция является взаимно однозначной. Если 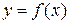взаимно однозначна, то каждому значению аргумента x соответствует одно значение y. Это означает, что существует функция
,
называемая обратной к функции .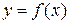
Из определения обратной функции следует, что
и 
Пример 16.1. Функция 
обратная к функции 
, для них справедливы равенства
и 
.
График обратной функции 
и график функции 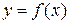симметричны относительно биссектрисы 1-й и 3-й четверти координатной плоскости, так как точке 
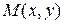графика функции соответствует точка 
графика обратной функции (см. рис. 1).
Рис. 1. Построение графика обратной функции.
Определение 16.7. Функция 
, у которой аргумент является функцией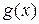 
, называется сложной, а сама операция получения сложной функции называется композицией.
Пример сложной функции: 
.
Определение 16.8. Основными элементарными функциями называются степенная, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции.
Определение 16.9. Элементарной функцией называется всякая функция, построенная из конечного числа основных элементарных функций, связанных между собой четырьмя арифметическими операциями и операцией композиции.
Пример 16. 2. 
‑ сложная функция.
Определение 16.10. Функция называется ограниченной на числовом множестве D, если для всех x из этого множества справедливо неравенство 
, где 
.
Определение 16.11. Функция называется ограниченной сверху на числовом множестве D, если для всех x из этого множества выполняется неравенство 
, где M некоторое число.
Определение 16.12. Наименьшее из чисел M, таких что для всех x из множества D, называется максимумом функции на множестве D.
Определение 16.13. Функция называется ограниченной снизу на числовом множестве D, если для всех x из этого множества выполняется неравенство 
, где M некоторое число.
Определение 16.14. Наименьшее из чисел M, таких, что для всех x из множества D, называется минимумом функции на множестве D.
Пример 16.3. Функция 
ограничена сверху на полуинтервале 
, так как 
на этом множестве. Максимум функции этом множестве равен 0 и достигается в точке 
.
