Вопрос 21.1. Теорема Лагранжа.
Теорема 21.1. (Теорема Лагранжа). Если  непрерывна на отрезке
непрерывна на отрезке  и дифференцируема внутри отрезка, то найдется хотя бы одна точка c такая, что
и дифференцируема внутри отрезка, то найдется хотя бы одна точка c такая, что  и
и

Эта формула носит название формулы конечных приращений Лагранжа (см. рис. 1).
Доказательство. Пусть  , тогда функции
, тогда функции  и
и 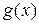 удовлетворяют условиям теоремы Коши. Применяя формулу Коши, получим
удовлетворяют условиям теоремы Коши. Применяя формулу Коши, получим

откуда следует формула Лагранжа

Конец доказательства.

Рис. 1. К доказательству теоремы Лагранжа.
Следствия из теоремы Лагранжа.
Следствие 21.1. Если  для всех x из интервала
для всех x из интервала  , то
, то  на интервале
на интервале  .
.
Доказтельство. Возьмем две произвольные точки  из интервала
из интервала  и применим формулу Лагранжа
и применим формулу Лагранжа  . Так как
. Так как 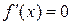 , то
, то  и, следовательно,
и, следовательно,  . Таким образом,
. Таким образом,  .
.
Конец доказательство.
Следствие 21.2. Пусть  на интервале
на интервале  , тогда
, тогда  монотонно возрастает (убывает) на интервале
монотонно возрастает (убывает) на интервале  .
.
Доказательство. Пусть  на интервале
на интервале  , тогда для любых точек
, тогда для любых точек  из этого интервала
из этого интервала  , то есть
, то есть  , если
, если  . Аналогично рассматривается случай
. Аналогично рассматривается случай  .
.
Конец доказательства.
Следствие 21.3. Пусть  на интервале
на интервале  , тогда
, тогда  монотонно не убывает (не возрастает) на этом интервале.
монотонно не убывает (не возрастает) на этом интервале.
Доказательство аналогично доказательству следствия 21.2.
Следствие 21.4. Если  на интервале
на интервале  , то для непрерывной на отрезке
, то для непрерывной на отрезке  и дифференцируемой на
и дифференцируемой на  функции
функции  справедливо неравенство
справедливо неравенство  .
.
Доказательство. По формуле Лагранжа  . Тогда
. Тогда  . Отсюда
. Отсюда  .
.
Конец доказательства.
Вопрос 21.2. Правила Лопиталя - Бернулли.
Теорема 21.2. Пусть  и
и 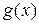 дифференцируемы на интервале
дифференцируемы на интервале  и являются бесконечно малыми функциями в окрестности точки a. Если существует (конечный или бесконечный) предел
и являются бесконечно малыми функциями в окрестности точки a. Если существует (конечный или бесконечный) предел  , то существует и предел
, то существует и предел  , причем оба предела равны.
, причем оба предела равны.
Доказатедьство. Так как  и
и 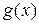 бесконечно малые функции, то
бесконечно малые функции, то 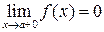 и
и  . Переопределим функции в точке x=a, положив
. Переопределим функции в точке x=a, положив  . Возьмем любую сходящуюся к a последовательность аргументов из отрезка [a,b]
. Возьмем любую сходящуюся к a последовательность аргументов из отрезка [a,b]  . Применяя к отрезку
. Применяя к отрезку  теорему Коши, получим
теорему Коши, получим

Так как  , то последовательность
, то последовательность  сходится к a. Поэтому получим
сходится к a. Поэтому получим

Отсюда следует доказываемая теорема.
Конец доказательства.
Замечание. Теорема с соответствующими изменениями справедлива при  .
.
Пример 21.1.  .
.
Конец примера.
Теорема 21.3. Пусть  и
и 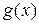 дифференцируемы на интервале
дифференцируемы на интервале  и являются бесконечно большими функциями в окрестности точки a. Если существует (конечный или бесконечный) предел
и являются бесконечно большими функциями в окрестности точки a. Если существует (конечный или бесконечный) предел  , то существует и предел
, то существует и предел  , причем оба предела равны.
, причем оба предела равны.
Замечание. Теорема с соответствующими изменениями справедлива при  .
.
Пример 21.2.


Конец примера.
Замечание. Если для 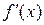 и
и  выполняются условия одной из теорем, то правила Лопиталя-Бернулли можно применять дважды и более число раз
выполняются условия одной из теорем, то правила Лопиталя-Бернулли можно применять дважды и более число раз

Пример 21.3.

Конец примера.






