(6)
Здесь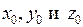 
‑ координаты точки M, лежащей на плоскости P, A, B и C ‑ координаты вектора, перпендикулярного плоскости P. Этот вектор называется нормальным к плоскости P (см. рис. 1).
Рис. 1. К выводу общего уравнения плоскости.
Уравнение (6) легко выводится из уравнения (5). Действительно, пусть точка 
лежит на плоскости P. Тогда ее координаты удовлетворяют уравнению
. (7)
Вычитая из уравнения (5) уравнение (7) и группируя слагаемые, получим уравнение (6). Рассмотрим теперь два вектора с координатами 
и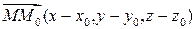 
соответственно. Из формулы (6) следует, что их скалярное произведение равно нулю. Следовательно, вектор перпендикулярен вектору 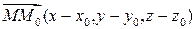. Начало и конец последнего вектора находятся соответственно в точках 
и 
, которые принадлежат плоскости P. Следовательно, вектор перпендикулярен плоскости P.
Расстояние от точки до плоскости P, общее уравнение которой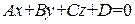 
, определяется по формуле
(8)
Доказательство этой формулы полностью аналогично доказательству формулы расстояния между точкой и прямой (см. рис. 2).
Рис. 2. К выводу формулы расстояния между плоскостью и прямой.
Действительно, расстояние d между прямой и плоскостью равно
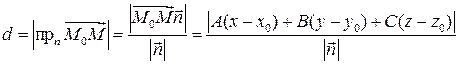
где 
‑ точка лежащая на плоскости. Отсюда, как и в лекции № 11, получается выше приведенная формула. Две плоскости параллельны, если параллельны их нормальные вектора. Отсюда получаем условие параллельности двух плоскостей
(9)
где
‑ коэффициенты общих уравнений плоскостей 
. Две плоскости перпендикулярны, если перпендикулярны их нормальные вектора, отсюда получаем условие перпендикулярности двух плоскостей, если известны их общие уравнения
(10)
Угол f между двумя плоскостями равен углу между их нормальными векторами (см. рис. 3) и может, поэтому, быть вычислен по формуле
Рис. 3. Определение угла между плоскостями.
(11)
Уравнение плоскости, проходящей через три заданные точки.
Рис. 4. Плоскость, проходящая через три точки 
.
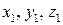‑ координаты заданной точки 
,
‑ координаты заданной точки 
,
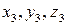‑ координаты заданной точки 
.
Действительно, пусть даны три точки . Пусть 
произвольная точка плоскости P. Тогда вектора
лежат в одной плоскости, следовательно, их смешанное произведение равно нулю, что и выражает равенство (12).
ЛЕКЦИЯ № 13. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Вопрос 13.1. Прямая в пространстве. Уравнение прямой в пространстве.
Общее уравнение прямой.
Прямая может рассматриваться как пересечение двух плоскостей (см. рис. 1). Пусть каждая плоскость задана общим уравнением, тогда прямая L задается общими
Рис. 1. К выводу уравнений прямой в пространстве.
уравнениями
(1)
где коэффициенты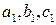 
не пропорциональны коэффициентам 
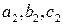. Последнее условие является условием непараллельности двух плоскостей. Вектора 
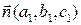и 
- являются нормальными к плоскости 
и 
. Следовательно, эти вектора перпендикулярны и самой прямой L.
