Вопрос 8.1. Проекция вектора на направленную ось.
Определение 8.1. Декартовой системой координат называется система координат, базисные вектора которой взаимно перпендикулярны и имеют единичную длину. Координаты вектора в такой системе называются декартовыми.
Определение 8.1. Проекцией вектора 
на вектор 
(на направленную ось) называют число
Следующая теорема раскрывает геометрический смысл проекции вектора
Теорема 8.1. Проекция вектора на направленную ось равна длине отрезка AB, заключенного между перпендикулярами, опущенными на направленную ось , если вектор одинаково направлены, и равна длине отрезка AB, если эти вектора направлены в противоположные стороны (см. рис. 1).
Доказательство. Пусть вектора и одинаково направлены. Тогда проведем через точку K, начало вектора , прямую, параллельную направленной оси . Из прямоугольного треугольника KLM следует, что (см. рис. 1 a))
Рис. 1. К доказательству теоремы 1.
a) векторы и одинаково направлены.
b) векторы и направлены в противоположные стороны.
Так как 
, то 
Пусть теперь вектора и направлены в противоположную сторону. Тогда из рис. 1 b) следует, что
но угол f между векторами и и угол g связаны соотношением:
Тогда получаем 
. Отсюда находим
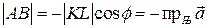
Конец доказательства.
Свойства проекции:
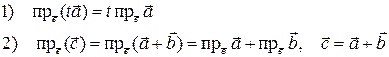
Доказательство первого свойства сразу следует из определения проекции вектора на направленную ось. Доказательство второго свойства следует из рис. 2., на котором изображены четыре
Рис 2. К обоснованию равенства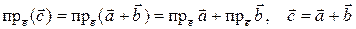 
.
возможных случая расположения векторов 
. Действительно, пусть вектора расположены так, как на рис. 2 a), тогда получаем
Аналогично рассматриваются остальные три случая b), c) и d).
Вопрос 8.2. Скалярное произведение векторов.
Определение 8.3. Скалярным произведением векторов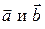 
называется произведение длин этих векторов на косинус угла между ними
.
Скалярное произведение обозначается также другим символом 
.
Свойства скалярного произведения:
Доказательство этих свойств очевидно и основано на определении скалярного произведения и свойств проекции вектора на направленную ось.
Для декартовой системы координат очевидно выполнение равенств
Тогда получаем для вектора: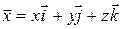 
Таким образом, декартовы координаты – это проекции вектора на координатные оси.
Пусть известны в декартовом базисе координаты векторов 
:
тогда
Таким образом,
Отсюда получаем
и
Пример 8.1. Вычислить угол между векторами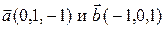 
.
Находим 
. Тогда 
или 
.
Конец примера.
Пример 8.2.
Механический смысл скалярного произведения:
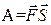‑ работа силы 
по перемещению тела на вектор перемещения 
.
Конец примера.
