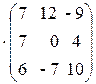Нехай визначник має n рядків і n стовпців. Мінором  k-го порядку k
k-го порядку k 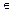 [1; n –1] називається визначник, утворений з елементів, розміщених на перетині будь-яких k рядків і k стовпців визначника. Зрозуміло, що мінор першого порядку — це будь-який елемент визначника.
[1; n –1] називається визначник, утворений з елементів, розміщених на перетині будь-яких k рядків і k стовпців визначника. Зрозуміло, що мінор першого порядку — це будь-який елемент визначника.
Приклад 1.2. Утворити кілька мінорів другого і один мінор третього порядку такого визначника:
 .
.
 ,
,  ,
,  ,
,  .
.
Верхній індекс означає нумерацію мінорів; нижній індекс — порядок мінора.
Доповняльним мінором для мінора k -го порядку називається такий мінор, який лишається у визначнику після викреслювання тих k рядків і тих k стовпців, на перетині яких містяться елементи, що утворили мінор k -го порядку.
Нехай мінор k- го порядку утворено з елементів, розміщених на перетині i 1, i 2,..., ik рядків і j 1, j 2,..., jk стовпців.
Алгебраїчним доповненням 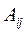 до мінора k -го порядку є допов-няльний мінор (n – k) - го порядку, узятий зі знаком
до мінора k -го порядку є допов-няльний мінор (n – k) - го порядку, узятий зі знаком 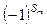 , де
, де 
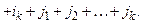 Якщо сума
Якщо сума 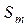 номерів рядків і стовпців парна, то береться знак «+», якщо непарна — то знак «–».
номерів рядків і стовпців парна, то береться знак «+», якщо непарна — то знак «–».
Далі важливу роль відіграватиме алгебраїчне доповнення до мінора першого порядку. Нехай 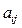 — будь-який елемент-мінор першого порядку у визначнику n -го порядку, тоді
— будь-який елемент-мінор першого порядку у визначнику n -го порядку, тоді  буде алгебраїчним доповненням до мінора
буде алгебраїчним доповненням до мінора 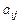 . Тут
. Тут  — доповняльний мінор (n –1)-го порядку, утворений викреслюванням i -рядка і j -стовпця в початковому визначнику n -го порядку.
— доповняльний мінор (n –1)-го порядку, утворений викреслюванням i -рядка і j -стовпця в початковому визначнику n -го порядку.
Обчислення визначників
Означення. Визначником n-го порядку називається число  , яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпця на відповідні їм алгебраїчні доповнення:
, яке дорівнює алгебраїчній сумі добутків елементів будь-якого рядка або стовпця на відповідні їм алгебраїчні доповнення:
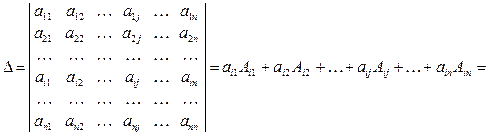
(1.4)

Алгебраїчні доповнення, що входять до формули (1.4), за якою обчислюють визначник, у свою чергу, є, мінорами, узятими з відповідними знаками, тобто визначниками (n –1)-го порядку. Отже, обчислення визначника n -го порядку зводиться до обчислення n визначників (n –1)-го порядку.
Але з формули (1.4) випливає, що за наявності у визначнику нульових елементів відповідні алгебраїчні доповнення обчислювати не потрібно.
Згідно з властивістю 8, яка справджується для визначників будь-якого порядку, можна визначник перетворити так, щоб у його рядках або стовпцях усі елементи, крім одного, дорівнювали нулю. Тоді, розклавши визначник за елементами цього рядка або стовпця, зведемо задачу знаходження визначника n-го порядку до знаходження одного визначника n–1-го порядку.
Приклад 1.3. Обчислити визначник:
 .
.
Розв’язання.
Обчислюємо визначник, розкладаючи його по елементам першого рядка.
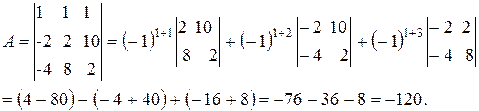
Матриці
Основні поняття
Розглянемо ще один математичний об’єкт, пов’язаний із системою рівнянь (1.1).
Означення. Матрицею називається прямокутна таблиця чисел, яка має m рядків і n стовпців. Якщо повернутися до системи рівнянь (1.1), то коефіцієнти при невідомих у лівій частині якраз і утворюють таку прямокутну таблицю:
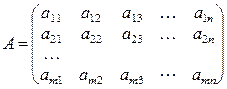 .
.
Числа  називаються елементами матриці, а запис
називаються елементами матриці, а запис  означає її розмір. Зауважимо, що на першому місці в цьому запису зазначено кількість рядків матриці, а на другому — кількість стовпців. Наприклад, запис розміру матриці
означає її розмір. Зауважимо, що на першому місці в цьому запису зазначено кількість рядків матриці, а на другому — кількість стовпців. Наприклад, запис розміру матриці 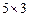 означає, що в ній п’ять рядків і три стовпці. Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною.
означає, що в ній п’ять рядків і три стовпці. Якщо кількість рядків матриці дорівнює кількості її стовпців, то матриця називається квадратною.
Дві матриці рівні між собою, якщо вони мають однаковий розмір і всі їх відповідні елементи рівні між собою.
Елементи з двома однаковими індексами a 11, a 22, a 33, ... ann утворюють головну діагональ матриці. Якщо 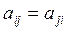 , то матриця називається симетричною.
, то матриця називається симетричною.
Квадратна матриця, в якої елементи головної діагоналі дорівнюють одиниці, а всі інші нулю, називається одиничною матрицею:
 .
.
Коли всі елементи матриці, що містяться по один бік від головної діагоналі, дорівнюють нулю, то матриця називається трикутною.
Кожній квадратній матриці можна поставити у відповідність визначник, який складається з тих самих елементів.
Якщо такий визначник відмінний від нуля, то матриця називається неособливою, або невиродженою. Якщо визначник дорівнює нулю, то матриця особлива, або вироджена.
Дії з матрицями
1. Сумою матриць одного й того самого порядку  і
і 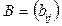 називається матриця
називається матриця  ;
;  , будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В:
, будь-який елемент якої дорівнює сумі відповідних елементів матриць А і В: 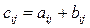 . Наприклад обидві матриці
. Наприклад обидві матриці 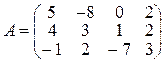 ,
,  мають розмір
мають розмір 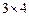 , тому за означенням можна утворити їх суму — матрицю
, тому за означенням можна утворити їх суму — матрицю
 .
.
2. Добутком матриці 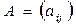 на деяке число
на деяке число  називається така матриця С, кожен елемент якої
називається така матриця С, кожен елемент якої 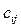 утворюється множенням відповідних елементів матриці А на
утворюється множенням відповідних елементів матриці А на  ,
,  .
.
Приклад 1.4.  ,
, 
 .
.
Очевидно, що для суми матриць і добутку матриць на число виконуються рівності:
1) 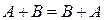 ;
;
2)  ;
;
3) 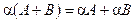 .
.
Добутком матриці  розміру
розміру 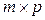 на матрицю
на матрицю 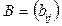 розміру
розміру 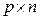 називається така матриця
називається така матриця  розміру
розміру 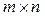 ,
, 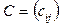 , кожний елемент якої можна знайти за формулою:
, кожний елемент якої можна знайти за формулою:
 .
.
Кожний елемент матриці С утворюється як сума добутків відповідних елементів і -го рядка матриці А на відповідні елементи j -го стовпця матриці В, тобто за схемою:

Зазначимо, що в результаті множення дістанемо матрицю розміру 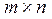 .
.
З означення випливає, що добуток матриць взагалі некомутативний: 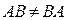 .
.
Приклад 1.5. Обчислити суму матриць А і В:
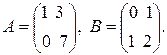
Розв’язання.

Приклад 1.6. Знайти добуток матриць А і В:
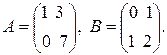
Розв’язання.

Якщо АВ = ВА, то матриці називаються переставними.
Одинична матриця переставна для всіх матриць її розмірності.
Транспонуванням матриці називається математична дія, коли рядки матриці А записуються стовпцями. Ця дія позначається як АТ, а матриця АТ називається транспонованою.
Приклад 1.7. Транспонувати матрицю 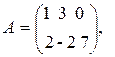 .
.
Розв’язання.
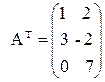 .
.
Обернена матриця
Якщо добуток двох квадратних матриць дорівнює одиничній матриці, тобто АС = Е, то матриця С називається оберненою по відношенню до А та позначається С = А—1. матриця А є оберненою до матриці С, тобто А=С-1. Тоді АА-1=А-1А=Е. Обернена матриця є переставною.
Властивості оберненої матриці:
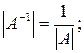
 – де
– де 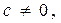
 ,
,
 .
.
Для знаходження оберненої матриці треба виконати такі дії.
1. Обчислити визначник матриці А. Якщо 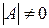 , то матриця називається невиродженою, і в цьому випадку існує обернена матриця.
, то матриця називається невиродженою, і в цьому випадку існує обернена матриця.
2. Обчислюються алгебраїчні доповнення кожного елемента а ij матриці А і записуються у вигляді матриці С.
3. Транспонується матриця алгебраїчних доповнень С.
4. Обчислюється обернена матриця за формулою:
 (1.4)
(1.4)
5. Виконується перевірка 
Приклад 1.8.
Знайти обернену матрицю для
 .
.
Розв’язання.
1. Обчислюємо визначник матриці А, розкладаючи його по першому рядку.
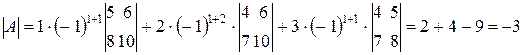 .
.
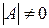 , тому обернена матриця існує.
, тому обернена матриця існує.
2. Обчислюємо алгебраїчні доповнення всіх елементів.
 ,
,
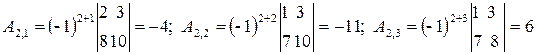 ,
,
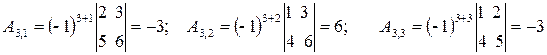 .
.
Запишемо матрицю алгебраїчних доповнень
 .
.
3. Транспонуємо матрицю С.
 .
.
4. Обернена матриця
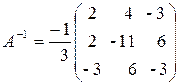 .
.
5. Перевірка.

Приклад 1.9. Знайти обернену матрицю для матриці
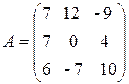
Розв’язання.
1. Обчислюємо визначник матриці А, дописавши два стовпця


 , тому обернена матриця існує.
, тому обернена матриця існує.
2. Обчислюємо алгебраїчні доповнення всіх елементів.
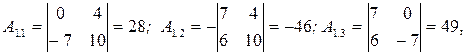 ,
,
 ,
,
 .
.
3. С - матриця алгебраїчних доповнень.
 .
.
4. Транспонуємо матрицю С.
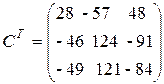 .
.
5. Обернена матриця.
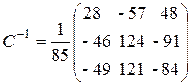 .
.
5. Перевірка