Розглянемо спочатку системи рівнянь, в яких кількість невідомих і кількість рівнянь рівні між собою, тобто m = n. Нехай, наприклад, n = m = 2, тоді маємо систему двох лінійних рівнянь з двома невідомими:
Визначником другого порядку називається вираз
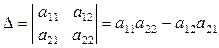. (1.2)
Приклад. 1.1
.
Якщо n = m = 3, то маємо систему трьох лінійних рівнянь з трьома невідомими:
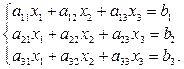
Визначником третього порядку називається вираз:
. (1.3)
Для запам’ятовування правила обчислення визначника третього порядку пропонуємо таку схему (правило трикутників):
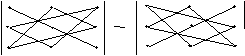
Позначимо точками елементи визначника, тоді доданки зі знаком «плюс» — це добутки елементів a 11, a 22, a 33, розміщених на головній діагоналі визначника, і добутки елементів a 13, a 21, a 32і a 12, a 23, a 31, розміщених у вершинах рівнобедрених трикутників, основи яких паралельні головній діагоналі. Зі знаком «мінус» беруться доданки, що є добутками елементів a 13, a 22, a 31, розміщених на сторонній діагоналі визначника, та у вершинах рівнобедрених трикутників, основи яких паралельні сторонній діагоналі визначника — a 11, a 23, a 32 і a 12, a 21, a 33.
Запропонуємо ще одне правило обчислення визначника третього порядку (правило Саррюса).
У початковому визначнику за третім стовпцем запишемо ще раз перший і другий стовпці:
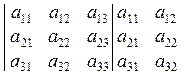
Для знаходження визначника за цим правилом треба утворити зі знаком «плюс» алгебраїчну суму добутків елементів, розміщених на головній діагоналі визначника, і на діагоналях, паралельних їй, а зі знаком «мінус» — добутків елементів, розміщених на сторонній діагоналі, та на діагоналях, паралельних їй.
Визначник:
,
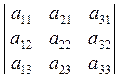рядки якого є стовпцями попереднього визначника, є транспонованим щодо визначника (1.3).
Властивості визначників
Властивість 1. Визначник не змінюється в результаті транспонування.
З властивості 1 випливає, що будь-яке твердження, котре справджується для рядків визначника, справджується і для його стовпців, і навпаки.
Властивість 2. Якщо один із рядків визначника складається лише з нулів, то такий визначник дорівнює нулю.
Властивість 3. Якщо поміняти місцями будь-які два рядки визначника, то його знак зміниться на протилежний.
Властивість 4. Визначник, який має два однакові рядки, дорівнює нулю.
Властивість 5. Якщо елементи будь-якого рядка визначника помножити на стале число С, то й визначник помножиться на С.
З останньої властивості випливає, що спільний множник елементів рядка можна виносити за знак визначника.
Властивість 6. Визначник, який має два пропорційні рядки, дорівнює нулю.
Властивість 7. Якщо всі елементи будь-якого рядка визначника можна подати у вигляді суми двох доданків, то такий визначник дорівнює сумі двох визначників, у яких елементами цього рядка будуть відповідно перший доданок у першому визначнику і другий доданок у другому визначнику, а решта елементів будуть ті самі, що й у початковому визначнику.
Властивість 8. Визначник не зміниться, якщо до елементів будь-якого рядка додати відповідні елементи довільного іншого рядка, попередньо помножені на деяке число.
