Модель системы аксиом T представляет собой такую совокупность некоторых объектов и отношений между ними, для которой выполняются все требования системы аксиом T, [9, с. 117–118].
Модель или реализация системы аксиом T называется также моделью или реализацией как аксиоматической теории 
, так и структуры 
. Эту реализацию будем обозначать R (T)= R (T 
, …, T 
).
Приведем примеры реализаций.
Модель линейного порядка Торальфа Сколема (см. п. 1.1 §1) является моделью, или реализацией, аксиоматики Пеано или структуры натурального ряда.
Множество действительных чисел является реализацией евклидовой прямой.
Арифметическая модель векторного пространства 
(см. п. 3.2 §3) является реализацией системы аксиом векторного пространства размерности три.
Арифметическая модель евклидова пространства 
(см. п. 4.1 §4) является реализацией как системы аксиом Гильберта, так и системы аксиом Вейля евклидовой геометрии.
Множество n –местных наборов чисел (x ,…, x ) является реализацией n –мерного арифметического евклидова пространства 
(см. п. 4.2 §4).
Модель Пуанкаре L 
является реализацией планиметрии Лобачевского.
Замечание 1
Понятия «модель» и «структура» часто используются как понятия «конкретного множества» и «множества с заданными свойствами». Именно в таком контексте мы использовали эти понятия в §3–5. Это не вступает в противоречие с точными определениями этих понятий, приведенными в этом §6.
6.4. Формальная и содержательная аксиоматики.
Теории и структуры
Пусть R (T) – реализация некоторой системы аксиом Т. Рассмотрим подробнее, что означает реализация R 
аксиоматической структуры 
. Согласно определению реализации, данному в предыдущем п. 6.3, объект R содержит:
некоторые объекты Ri (Mi), являющиеся реализациями базовых множеств M 1…, Mm так, что существует взаимно однозначное соответствие xi 
ri (xi) между элементами xi 
Mi и элементами ri Ri, i = 1,2,…, m;
некоторые отношения pi (r 1,…, rm), представляющие или отражающие отношения Ði(x 1,…, xm) соответствующих элементов xi ri (xi);
некоторые объекты R (T), представляющие или отражающие в виде некоторых отношений утверждения в системе аксиом Т (обычно R (T) называют реализацией системы аксиом).
Рассмотрим пример
Пусть R 2 – арифметическая модель евклидовой плоскости. Тогда базовое множество М 1 – это все точки M R 2, реализующиеся как упорядоченные числовые пары (x, y). Множество H 2 – это множество всех прямых l 
R 2, реализующихся уравнениями вида ax + by + c = 0. Отношение Ð1(M, l) 
(M l) – точка М принадлежит прямой l, реализуется свойством P 1: пара (x, y) удовлетворяет уравнению ax + by + c = 0, и т.д.
Вывод 1
Всякая реализация R (T) системы аксиом Т устанавливает взаимно однозначное соответствие xi ri (xi) между элементами xi базовых множеств Mi и объектами ri реализаций Ri (Mi), базовых множеств. При этом отношения Ði(x 1,…, xm) между элементами xi Mi , заданные в системе аксиом Т, представляются или реализуются некоторыми отношениями Pi (ri,…, rm) между соответствующими объектами ri (xi).
Вывод 2
Всякое утверждение А теории получается логическим заключением (выводом) и в реализации R (T) находится соответствующее отношение между объектами, отражающее утверждение А.
Определение
Система аксиом Т, ее аксиоматическая теория и аксиоматическая структура , определенные вне какой–либо реализации, называются абстрактными или формальными системой аксиом, теорий или структурой соответственно.
Если существует реализация R(T) этой системы, то система Т, теория и структурой называются содержательными.
Классическим примером формальной теории является геометрия Лобачевского. Эта мыслимая геометрия долгое время не воспринималась однозначно как аксиоматическая теория, пока не были найдены ее реализации, например, реализация Пуанкаре L 2, построенная в п.6. Таким образом, исторический опыт с геометрией Лобачевского имеет "хороший конец": были найдены реализации и сняты все вопросы в рамках этих реализаций.
Чтобы использовать реализации R (T) для исследования аксиоматических систем Т, введем понятие изоморфизма реализаций (структур).
Изоморфизм
Пусть система аксиом Т имеет две реализации R (T) и R '(T). Тогда согласно выводу 1 (п.6.4) между объектами Ri и R ' i реализующими базовые множества Мi, устанавливается взаимно однозначное соответствие по схеме
(2)
Что можно сказать о соответствии между реализациями соотношений Рi в Ri и реализациями отношений P ' i в R ' i? Рассмотрим два примера.
Пример 1
Пусть система аксиом Т состоит из 14 аксиом аксиоматики Гильберта, определяющих абсолютную геометрию плоскости (геометрию без аксиомы параллельности). Мы имеем две реализации этой планиметрии:
арифметическая модель R 2 (евклидовой плоскости);
модель Пуанкаре L 2 (плоскости Лобачевского). Можно установить взаимно однозначное соответствие между точками М R 2 и точками N L 2, а также между прямыми l R 2 и прямыми a L 2. В то же время не всем отношениям между точками и прямыми в L 2 можно найти соответствующие отношения в R 2. Например, отношение Ð(a 1, a 2) 
прямые a 1 и a 2 не параллельны и не пересекаются 
может выполняться в L 2 и не имеет аналога в R 2. (Другие неевклидовы отношения между точками и прямыми на плоскости L 2 см. в п. 5.2 §5).
Пример 2
Пусть e2 – геометрическая модель направленных отрезков (выполненная, например, карандашом на бумаге или реализованная на мониторе компьютера). Пусть Е 2– арифметическая модель векторного пространства. Операция откладывания вектора, указанная в модели Вейтеля (п.4.1 §4), устанавливает взаимно однозначное отображение 
: 
(x, y) модели e2 
на модель Е 2 (x, y). При этом, отображение сохраняет все определенные в векторной структуре отношения между соответствующими векторами и ()=(x, y).
Определение изоморфизма
Две реализации R (T) и R '(T) системы аксиом Т будем называть изоморфными, если выполняется два условия:
существует взаимно–однозначное соответствие (2) между реализациями Ri (Mi) и R ' i (Mi) базовых множеств Mi, i =1,2,…, m;
отображение (2) устанавливает взаимно однозначное соответствие между всеми свойствами P ' i (r '1,…, r ' m) и Pi (r 1,…, rm), представляющими в моделях R и R ' свойства Ði(x 1,…, xm) соответствующих при отображении (2) элементов r ' i 
xi ri.
Само отображение (2) при этом называется как изоморфизмом моделей или реализацией R (T) и R '(T), так и изоморфизмом аксиоматических структур 
T; P; R и 
T; P '; R ' .
Другими словами, изоморфизм моделей – это такое взаимно однозначное соответствие между элементами моделей, которое сохраняет отношения элементов, задаваемые системой аксиом.
В примере 1, приведенном выше, модели R 2 и L 2 не изоморфны. В примере 2 модели e2 и E 2 изоморфны.
Вывод 3
Если систему аксиом Т и ее аксиоматическую теорию рассматривать как мыслимые или абстрактные объекты, и если существует реализация R (T) этой системы Т, то соответствие между элементами базового множества М и элементами объекта R (M), реализующего М, устанавливает изоморфизм между мыслимой структурой T,Ð; М и моделью этой структуры 
T; P; R (M) .
Вывод 4
Разница между абстрактной (формальной) системой аксиом с некоторой реализацией и содержательной системой аксиом состоит только в способе построения структуры. Действительно, можно вначале построить абстрактную систему аксиом, а затем указать ее модель. Можно наоборот, вначале выбрать те свойства модели, которые определяют ее с точностью до изоморфизма, а затем эти свойства принять за аксиомы. Оба способа определяют две изоморфные структуры.
Вывод 5
Всякая аксиоматическая структура 
T,Ð; М определена с точностью до изоморфизма. Это означает, что любая ее изоморфная модель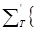 
T; P; R (M) рассматривается как совокупность тех и только тех свойств, которые выводятся логическим путем в теории .
