Плоскостью Лобачевского называется мыслимая планиметрия, определяемая аксиомами 1 – 3 группы I, всеми аксиомами групп II – IV системы аксиом Д. Гильберта и аксиомой параллельности V’ Лобачевского.
Эта модель неевклидовой геометрии была опубликована Н. И. Лобачевским в его известной работе «О началах геометрии» в журнале «Казанский вестник» в 1829–1830 г. г. Созданная им геометрия получила название мыслимой геометрии, так как в течение длительного времени в математическом мире отсутствовала общепризнанная реализация этой модели.
То, что существует хотя бы одна прямая, проходящая через точку A вне прямой a и не пересекающая прямую a, было доказано еще Евклидом без ссылки на постулат о параллельности (см. замечание 3 §3). Одна из моделей, в которой через точку A вне прямой a проходит более одной прямой, не имеющей общих точек с a, была построена великим французским математиком Жюлем Анри Пуанкаре (1854–1912). Эта модель (опубликована около 1883 г.) представляет множество точек полуплоскости, на которой «прямые» определены так, что реализуются все 15 аксиом планиметрии Лобачевского.
Рассмотри кратко эту модель, опуская доказательства, которые можно найти, например, в [7].
Представление основных объектов – точек и прямых в модели Пуанкаре. Пусть l – произвольная прямая евклидовой плоскости. Точками плоскости Лобачевского будем называть все точки одной из полуплоскостей, например, верхней, лежащих по одну сторону от l. Прямыми плоскости Лобачевского назовем либо вертикальные лучи, лежащие в заданной полуплоскости, либо полуокружности с центрами на l, также лежащими в этой полуплоскости, (рис. 8).
 |
Прямая l представляет «бесконечно удаленные точки» плоскости Лобачевского и называется абсолютом.
Углы между прямыми – это обычные евклидовы углы, образованные касательными в точке пересечения полуокружностей, представляющих эти прямые (рис. 8).
Движение в модели Пуанкаре плоскости Лобачевского представляется специальными дробно–линейными преобразованиями верхней полуплоскости на себя. Это преобразование сохраняет отношение 4 точек, через которое определяется функция расстояния между двумя точками в модели Пуанкаре. Мы не будем иллюстрировать свойства конгруэнтности на плоскости Лобачевского, поэтому не приводим формулы, представляющие функцию расстояния. Подробно изложение свойств движения в модели Пуанкаре плоскости Лобачевского можно найти, например, в [7].
В модели, определяемой перечисленными выше условиями 1–4, выполняются все 15 аксиом планиметрии Лобачевского. Эту модель будем обозначать L 2 и ограничимся проверкой нескольких аксиом.
Проверим две первые аксиомы I группы. Они должны определять единственную прямую в модели L 2 по двум любым точкам. Пусть абсолют l – линия OX в евклидовой плоскости. Тогда уравнения окружностей с центром в точках A (x 0, О) Î l и радиусом R имеют вид
(x – x 0)2 + y 2 = R 2. (5)
Две точки B (x 1, y 1), C (x 2, y 2) лежат на некоторой «прямой» a тогда и только тогда, когда их координаты удовлетворяют уравнению (5) для некоторых значений x 0 и R:
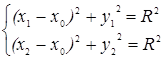(6)
В полученной алгебраической системе уравнений числа x 1, y 1 и x 2, y 2 заданы, а величины x 0 и R – искомые. Раскрывая квадраты и вычитая второе уравнение из первого, находим
x 12 – x 22 + y 12 – y 22 = 2 x 0(x 1 – x 2).
Откуда
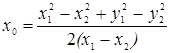
Это решение определено, если x 1¹ x 2, т.е. точки B и C не лежат на общем перпендикуляре x 1= x 2= х к оси OX. (Если x 1= x 2= x, то этот перпендикуляр представляет прямую в L 2 (рис. 9, а)). Подставляя найденное значение x 0, в любое из уравнений (6), находим значение радиуса R. Тем самым найдена окружность (5), проходящая через точки B и C. Эта окружность единственная и в модели L 2 представляет единственную же «прямую» a, инцидентную точкам B и C (рис. 9, b).
 |
Таким образом, аксиомы 1 и 2 группы I выполнены. Аксиома 3 этой группы выполняется очевидным образом.
Оставляя проверку аксиом группы II–IV, займемся проверкой аксиомы V' (параллельности по Лобачевскому) в модели L 2. Пусть a – некоторая прямая и точка A Ïa в модели L 2, рис.3. Пусть A ¥ и B ¥ – точки на абсолюте l, представляющие бесконечно удаленные точки прямой a (рис. 10). Используя формулу (5) точно так же, как при проверке аксиом 1–2 группы I, заключаем, что существует единственная окружность с центром на l, проходящая через точки A и A ¥, обозначим ее g1(A, A ¥), и, аналогично, единственная окружность g2(A, B ¥) (рис. 10). Полуокружности g1 и g2 в верхней полуплоскости L 2 представляют две прямые, параллельные прямой a, так как имеют с ней общие точки A ¥=g1Ça и B ¥=g2Ça, лежащие на абсолюте l и являющиеся, по определению, бесконечно удаленными точками. Кроме этого, существует еще бесконечно много прямых g, представляемых окружностями, проходящими через точку A внутри вертикального угла, образованного g1, и g2 (рис. 10). Эти прямые не имеют общих точек с a в L 2 даже на абсолюте и называются прямыми, расходящимися с a.
Следствие 1
В плоскости L 2 через точку A вне прямой a проходит бесконечное множество прямых, не имеющих общих точек с a (расходящихся с a). При этом существует в точности две параллельные g1 и g2, имеющие общие точки с a на абсолюте l
A ¥ = g1 Ç aÎ l, A ¥ = g2 Ç aÎ l,
Вывод
В модели L 2 выполняются 15 аксиом планиметрии Лобачевского.
Основные факты в планиметрии Лобачевского
Принятие столь экзотической аксиомы параллельности V' позволяет «обнаружить» (точнее, строго доказать) на плоскости L 2 неевклидовы «эффекты», т.е. такие отношения между геометрическими объектами, которые не реализуются в евклидовой плоскости.
Ограничимся иллюстрацией ряда свойств взаимного расположения прямых на плоскости L 2. Строгое доказательство этих фактов можно найти, например, в [7].
1. Сумма углов многоугольника в плоскости L 2
 |
Рассмотрим треугольник (рис. 11, а) с вершинами, лежащими на абсолюте. Так как, по определению абсолюта вершины, А 1, А 2, А 3 бесконечно удалены, то этот треугольник образован тремя сторонами А 1 А 2, А 1 А 3 и А 2 А 3 бесконечной длины. Так как в вершинах А 1, А 2 и А 3 окружности касаются друг друга, то представляемые ими «прямые» А 1 А 2, А 1 А 3 и А 2 А 3 образуют нулевые углы между собой. Аналогично, на рис. 11, b представлен n –угольник с бесконечно длинными сторонами и суммой углов, равной нулю.
Если внутренние окружности на рис. 11, a и b взять чуть большего радиуса, то точки А 1 А 2… Аn попадут в плоскость L 2 (не будут лежать на абсолюте), перестанут считаться бесконечно удаленными. Тогда длины сторон многоугольника станут конечными, а сумма углов многоугольника станет несколько больше нуля. С другой стороны, если треугольник образован «малыми» кусками дуг окружностей (рис. 11, с), то сумма его углов приближается к 180°, но остается все же несколько меньше 180°.
Следствие 2
В плоскости Лобачевского L2 сумма углов треугольника не постоянна и может принимать любое значение больше нуля и меньше p.
2. Взаимное расположение прямых в плоскости L2
Всякие две прямые в плоскости L 2 либо пересекаются, либо параллельны, либо являются расходящимися, т.е. не параллельны и не пересекаются, рис. 3.
