Готлоб Фреге впервые обратил внимание на то, что имя каждого объекта имеет два значения: предметное и смысловое. Согласно его “теории смысла” с понятием имени связаны три отношения к объекту: предметное, смысловое и знаковое. Определим их:
Денотат имени – это предметное значение имени, т.е. сам именуемый объект.
Концепт имени – это смысловое значение имени, т.е. то объективное содержание, которое выражается именем.
Константы – это сами имена индивидуальных предметов, но не имена свойств и отношений.
Наличие у имен двух значений – предметного и смыслового – приводит к двузначности имени: если имеется в виду концепт имени, то говорят об интенциональном значении имени, если же имеется в виду денотат имени, то говорят об экстенциональном значении имени.
Рассмотрим примеры.
Пример 1
“Число 2” – это имя имеет определенный денотат и концепт.
Пример 2
Имена: “Отношение эквивалентности”, “подобие”, “параллельность” имеют определенный концепт, как некоторые отношения. В то же время денотаты этих имен не определены.
Пример 3
Имя “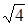 
“ – символ, представляющий определенный денотат – число 2. Однако, его концепт неопределен: 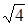– операция или 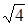– величина?
Проблема выразимости
Двузначность “имени” придает гибкость языку как средству коммуникации и в то же время делает его несовершенным как знаковое средство передачи информации. Действительно, последовательность слов как знаковых единиц накапливает неопределенность или многозначность от слова к слову.
В конце концов, смысл предложения как знаковой цепочки становится неопределенным. Мера определенности, по-видимому, является мерой символьной длины формального предложения, состоящего из знаков-слов.
Математики всегда сознавали несовершенство естественного языка. Громоздкие языковые конструкции затрудняли математическую деятельность, которая сводилась к описанию моделей, структур и изоморфизмов. Это послужило причиной возникновения символьного языка математической логики, предметных языков геометрии, теории множеств и т.д.
Однако символьный язык не смог полностью заменить естественный язык, так как язык изложения по необходимости всегда шире предметного языка самой теории.
Требование математической строгости, с одной стороны, заключается в изоморфном описании структур, т.е. требуется, чтобы некоторый минимум свойств-аксиом однозначно представлял объекты по их отношениям. С другой стороны, всякое рассуждение должно начинаться с явного описания соответствующей предметной области. Эти два требования, как правило, несовместимы. А эта несовместимость и порождает проблему выразимости.
