Арифметизация трехмерного евклидова пространства
Геометрической моделью трехмерного евклидова пространства будем называть множество точек, прямых плоскостей, удовлетворяющих двадцати аксиомам Д. Гильберта, сформулированным в §2. Эту модель будем обозначать e3 
и называть евклидовым пространством.
Построим арифметическую, или координатную, модель евклидова пространства e3, используя координатную модель евклидова векторного пространства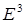 
, построенную в §3. Для этого введем операцию откладывания вектора. Эта операция сопоставляет всяким двум точкам A,B Îe3 вектор 
и обозначается как отображение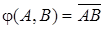 
. Операцию 
можно представить как изображение направленного отрезка и определить следующими основными свойствами.
Свойства операции откладывания вектора
Для всякой фиксированной точки A0 Îe3 и произвольной точки B Îe3 отображение 
(1)
является взаимно однозначным отображением точек B Îe3 на множество векторов 
.
.
(Аксиома реализуемости операции откладывания). Существует хотя бы одна точка 0Îe3, для которой определена операция откладывания вектора 
для любой точки 
.
Точку 
в аксиоме 3 называют началом координат в евклидовом пространстве e3, а вектор 
– радиус–вектором точки 
в этом пространстве. Координатами 
точки M Îe3 называют координаты радиус–вектора (рис. 7), где 
, 
, 
– направленные отрезки в e3, соответствующие базисным векторам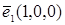 
, 
, 
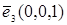векторного пространства при отображении (1) с 
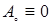. Таким образом, по построению операции откладывания вектора в e3 приходим к векторному равенству
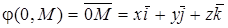. (2)
Это равенство, с учетом фиксированной точки 0Îe3, представляет взаимно однозначное соответствие между точками M Îe3 и арифметическими упорядоченными тройками чисел 
и является определяющим равенством для координат точек евклидова пространства.
Для вычисления длин отрезков и углов между ними воспользуемся свойствами скалярного произведения (4), (6), (7), (8) из §3, а также свойством 1 операции откладывания отрезка.
Пусть требуется найти длину отрезка 
, если заданы координаты его концов 
и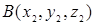 
. Учитывая, что 
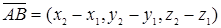, из формулы (8) § 3 находим длину
(3)
Пусть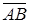 
= 
(u 1, v 1, w 1) и 
= 
(u 2, v 2, w 2) – направленные отрезки в e3 и пусть их координаты 
(u 1, v 1, w 1) 
(u 1, v 1, w 1) в Е3. Тогда, используя формулы (4), (7) и (8) из §3, получаем формулу для косинуса угла между и
(4)
Определение
Арифметической, или координатной, моделью евклидова пространства e3 называется множество упорядоченных троек чисел, определяемых соответствием ( 2 ) вместе с формулами длины отрезка ( З ) и углов между направленными отрезками ( 4 ), выраженными через скалярное произведение. Арифметическую модель трехмерного евклидова пространства будем обозначать R 3.
Вывод 1
Для построения модели R 3 требуется задать или построить:
геометрическую модель трехмерного векторного пространства (модель направленных отрезков e3);
изоморфную модель координатного векторного пространства Е 3;
операцию откладывания вектора (1);
скалярное произведение, посредством которого вычисляются длины и
углы.
Основные объекты геометрии – точки, прямые и плоскости в R 3 определяются на «языке» векторов и координат. Например, пусть плоскость П определяется точкой M 0(x 0, y 0, z 0) и вектором нормали (A, B, C). Это эквивалентно тому, что если М (x, y, z) – произвольная точка плоскости П, то 
, что эквивалентно условию (
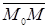
)=0, или в координатной форме П:
(x – x 0) A +(y – y 0) B +(z – z 0) C =0
Таким образом, искомая плоскость П в R 3 – это множество троек чисел (x, y, z), удовлетворяющих этому алгебраическому уравнению.
Аналогичным образом, в виде алгебраических соотношений представляются все геометрические объекты в R 3 и их метрические характеристики: длина, углы, площади и т.д.
Вывод 2
Решение геометрических задач в модели R 3 сводится к решению систем уравнений.
