Конструктивное построение множества действительных чисел можно представить в виде схемы 3.
 |
Непрерывными операциями мы называем вычислительные алгоритмы, состоящие из арифметических и других простых операций, пронумерованных натуральным рядом. Описание непрерывных операций потребует разработки вспомогательных понятий. Избежать такой дополнительной работы можно аксиоматическим заданием множества действительных чисел.
Добавим к аксиомам, определяющим в п. З. множество рациональных чисел Q, еще одну.
Аксиома непрерывности Кантора.
16. Пусть элементы x 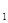 , x
, x  ,…, x
,…, x  ,…, y
,…, y 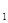 , y
, y  ,…, y
,…, y  ,… удовлетворяют условию x
,… удовлетворяют условию x 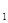 < x
< x  <…< x
<…< x  <…< y
<…< y  <… y
<… y  < y
< y 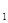 и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y
и пусть для любого положительного элемента e>0, начиная с некоторого номера n, выполняются условия y 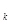 – x
– x 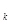 < e, k = n, n +1, …. Тогда существует элемент Z такой, что при всех значениях n выполняется x
< e, k = n, n +1, …. Тогда существует элемент Z такой, что при всех значениях n выполняется x  < Z < y
< Z < y  .
.
То, что элемент Z, о котором говорится в этой аксиоме, является единственным, несложно доказать от противного.
Определение 2
Множество R называется множеством действительных чисел, а его элементы действительными числами, если они удовлетворяют всем тем же аксиомам 1–15, что и рациональные числа и, дополнительно, аксиоме непрерывности Кантора.
О представлении действительных чисел
Мы видели, что формирование аксиоматик множеств натуральных рациональных и действительных чисел связано с выполнением определенных операций над числами. Система записи или представления чисел связана и с другими задачами.
Задача 1
Построить символьную запись числа, в которой эффективно реализуются алгоритмы арифметических и алгебраических операций. Мы уже отмечали, что наиболее подходящей для этой цели является систематическая запись числа (десятичная, двоичная и др.)
Задача 2
Построить представление чисел, в котором иррациональные числа приближаются рациональными числами наилучшим образом. Рациональная дробь p / q приближает иррациональное число a наилучшим образом, если для любого рационального числа m / n с n £ q выполняется равенство |a– p / q | < |a– m / n |.
Рассмотрим десятичные приближения. Пусть m = a  , a
, a 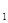 , …, a
, …, a 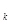 – десятичное приближение с “ k ” знаками после запятой числа a = a
– десятичное приближение с “ k ” знаками после запятой числа a = a  , a
, a 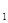 , …, a
, …, a 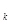 , a
, a 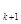 ,…. Тогда погрешность этого приближения определяется разностью
,…. Тогда погрешность этого приближения определяется разностью
|a– m / n | = a 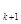 /10
/10 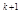 + a
+ a 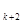 /10
/10 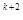 +…<9/10
+…<9/10 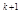 (1+1/10+…) = 9/10
(1+1/10+…) = 9/10 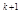 ´
´
1/(1–1/10) = 1/10  ~1/ n.
~1/ n.
Для лучших приближений используется представление иррационального числа цепной дробью [6]. Если p / q – конечная цепная дробь, приближающая число a, то ([6, с. 46]), |a– p / q | < 1/ q  .
.
Таким образом, представление числа цепной дробью «более экономично», чем представление десятичной дробью.
Напомним, что до сих пор не найдены эффективные алгоритмы арифметических операций для представлений чисел в виде цепных дробей, ([6, с. 29–30]).






