Конструктивное определение рациональных чисел Q дано в схеме 2 предыдущего пункта. Приведем аксиоматическое определение. Оно содержит тот минимум правил, который обеспечил построение множества Q в предыдущем пункте.
Определение 1
Множество Q называется множеством рациональных чисел, а его элементы – рациональными числами, если выполняется следующий комплекс условий, называемый аксиоматикой рациональных чисел:
Аксиомы операции сложения
Для всякой упорядоченной пары х,у элементов из Q определен некоторый элемент х+у Î Q 
, называемый суммой х и у. При этом выполняются следующие условия:
1. (Существование нуля) Существует элемент 0 (нуль) такой, что для любого х Î Q
х +0=0+ х = х.
2. Для любого элемента х Î Q существует элемент – х Î Q (противоположный х) такой, что
х + (–х) = (–х) + х = 0.
3. (Коммутативность) Для любых х,у Î Q
х + у = у + х.
4. (Ассоциативность) Для любых х,у,zÎ Q
х + (у + z) = (х + у) + z.
Аксиомы операции умножения
Для всякой упорядоченной пары х, у элементов из Q определен некоторый элемент ху Î Q, называемый произведением х и у. При этом выполняются следующие условия:
5. (Существование единичного элемента) Существует элемент 1 Î Q такой, что для любого х Î Q
х . 1 = 1 . х = х.
6. Для любого элемента х Î Q, (х 
0) существует обратный элемент х –1 0 такой же, что
х.х –1 = х–1. х = 1.
7. (Ассоциативность) Для любых х, у,z Î Q
х . (у . z) = (х . у) . z.
8. (Коммутативность) Для любых х, у Î Q
х. у = у. x.
Аксиома связи сложения и умножения
9. (Дистрибутивность) Для любых х, у, z Î Q
(х+у) . z = x . z+у . z.
Аксиомы порядка
Всякие два элемента х, у, Î Q вступают в отношение сравнения 
. При этом выполняются следующие условия:
10. (х у)L (у x) 
x=у.
11. (х у) L ( у z) 
x 
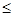z.
12. Для любых х, у Î Q либо х < у, либо у < x.
Отношение < называется строгим неравенством,
Отношение = называется равенством элементов из Q.
Аксиома связи сложения и порядка
13. Для любых x, y, z Î Q, (x £ y) Þ x + z £ y + z.
Аксиома связи умножения и порядка
14. (0 £ x)Ç(0 £ y) Þ (0 £ x ´ y).
Аксиома непрерывности Архимеда
15. Для любых a > b > 0 существует m Î N и n Î Q такие, что m ³ 1, n < b и a = mb + n.
Следствие
Аксиомы множества Q позволяют:
I. Построить систематическую запись рациональных чисел при помощи конечного алфавита (цифровых символов).
II. Определить алгоритмы реализации операций ±, ´,:, £ в систематической записи рациональных чисел.
1.4. Задачи, приводящие к расширению
множества рациональных чисел
Решение задач, имеющих практический интерес, не исчерпывается арифметическими операциями над числами. Рассмотрим следующие две задачи.
Задача 1
Измерить длину диагонали квадрата, считая, что единица длины есть сторона этого квадрата.
Теорема Пифагора дает результат: искомая длина равна 
. Предположение о том, что = p / q – рациональное число опровергается известным доказательством от противного. Предположим, что = k / q Þ p 
= 2 q Þ p =2 k Þ 2 q = 4 k Þ q = 2 m Þ = 
– сократимая дробь, что противоречит несократимости дроби 
= p / q.
Заметим, что величина является решением уравнения x –2=0. Действительные рациональные числа, являющиеся решениями алгебраических уравнений
x 
+ a 
x 
+ … + a 
x + a = 0 (10)
с целочисленными коэффициентами a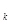 
Î Z, k =1, …, n, называются алгебраическими числами. Таким образом, число является алгебраическим числом и результатом алгебраической операции – извлечения корня.
Карл Фридрих Гаусс (1777 – 1855) доказал (см., например, ([4, с. 63])), что алгебраические числа являются либо целыми числами, либо не представимы в виде p / q ни для каких целых p, q Î Z.
Задача 2
Измерить длину окружности, считая, что диаметр этой окружности есть единица длины.
Длина окружности L = 2p R, где R – радиус. В нашем случае L =3,1415…. Число p не является ни рациональным, ни алгебраическим, [4]. То, что число p не является рациональным числом, впервые было установлено в 1761 г. французским математиком Иоганном Генрихом Ламбертом (1728 – 1777).
Подчеркнем, что число p не является результатом применения алгебраических операций. Оно может быть выражено согласно алгоритму Ф. Гаусса ([5, с. 41]), который представляет последовательность некоторых простых операций, пронумерованных числами натурального ряда.
Вывод 3
Существуют числа, не являющиеся результатом конечного числа арифметических операций над целыми числами и не представимые в виде p/q ни для каких целых p, q.
Числа, не представимые в виде p/q ни для каких целых p, q, называются иррациональными.
