При анализе медицинских, инженерных и научных данных часто возникает необходимость найти наклон кривой, которая задана таблицей значений.
Возможна и другая ситуация: f (x) известна, но имеет очень сложное аналитическое выражение.
В первом случае классические методы дифференциального исчисления просто неприемлемы, а во втором случае их использование вызывает значительные трудности. В таких задачах вместо функции f (x) рассматривают интерполирующую функцию P (x), а затем полагают f ' (x) » P' (x) на интервале a£x£b. Аналогично поступают при нахождении производных высших порядков функции f (x) .
Если для интерполирующей функции P (x) известна погрешность интерполяции R (x) =f (x) –P (x), то погрешность производной равна производной от погрешности этой функции
r (x) =f ' (x) –P' (x) =R' (x).
Такое утверждение справедливо и для производных высших порядков.
В целом же численное дифференцирование представляет собой операцию менее точную, чем интерполирование.
Формулы для вычисления первой производной
Численное дифференцирование весьма чувствительно к погрешностям, вызванным неточностью исходных данных. Значительно меньшую погрешность имеет дифференцирование многочленов наилучшего среднеквадратического приближения (методом наименьших квадратов). На практике часто применяются формулы безразностного дифференцирования для производной первого порядка:
По трем точкам:
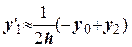(5.1)
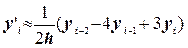
По четырем точкам:
; (5.2)
;
.
По пяти точкам:
;
;
; (5.3)
;
.
Формулы второй производной
По четырем точкам:
; (первое значение)
; (внутренние точки) (5.4)
. (последнее значение)
По пяти точкам:
;
;
; (5.5)
;
.
Заметим, что с ростом порядка производной резко падает точность численного дифференцирования. Поэтому на практике редко применяют формулы для производных второго порядка.
Примеры
№1. Пользуясь безразностными формулами по 3 точкам, определить первые производные для функции у=х 2 на интервале [1; 3] с шагом 0,2 и сравнить их значения с аналитическими.
Решение.
Воспользуемся формулами (5.1):
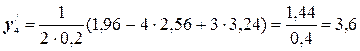
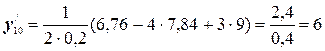
Для сравнения этих значений с аналитическими составим таблицу:
| i | хi | у=х 2 | Аналитические значения у΄=2х | Численные значения у΄ |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,44 1,96 2,56 3,24 4,84 5,76 6,76 7,84 | 2,4 2,8 3,2 3,6 4,4 4,8 5,2 5,6 | 2,0 2,4 2,8 3,2 3,6 4,4 4,8 5,2 5,6 |
Таким образом, мы видим, что все значения первой производной полностью совпадают с аналитическими.
№2. Пользуясь безразностными формулами по 4 точкам, определить первые производные для функции у=х 3 на отрезке [1; 3] с шагом 0,2 и сравнить эти значения с аналитическими.
Решение.
Пользуемся формулами (5.2):
и т.д. по формуле для 
.
Для сравнения полученных значений с аналитическими составим таблицу:
| i | хi | у=х 3 | Аналитические значения у´= 3 х 2 | Численные значения у´(х) |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,728 2,744 4,096 5,832 10,648 13,824 17,576 21,952 | 4,32 5,88 7,68 9,72 14,52 17,28 20,28 23,52 | 4,32 5,88 7,68 9,72 14,52 17,28 20,28 23,52 |
Получим, что для функции у=х 3 численное дифференцирование по 4 точкам дает такие же значения, что и аналитические.
№3. Найти вторую производную для функции у=х 3 на отрезке [1; 3] с шагом 0,2, пользуясь безразностными формулами по 4 точкам и сравнить полученные значения с аналитическими.
Решение.
Воспользуемся формулами (5.4):
(первое значение)
(последнее значение)
и т.д. по формуле для внутренних точек.
Для сравнения составим таблицу:
| i | хi | у=х 3 | Аналитические значения у″= 6 х | Численные значения у″ |
| 1,2 1,4 1,6 1,8 2,2 2,4 2,6 2,8 | 1,728 2,744 4,096 5,832 10,648 13,824 17,576 21,952 | 7,2 8,4 9,6 10,8 13,2 14,4 15,6 16,8 | 7,2 8,4 9,6 10,8 13,2 14,4 15,6 16,8 |
Таким образом, получим, что для функции у=х 3 численное нахождение второй производной по 4 точкам дает такие же значения, что и аналитические.
Варианты заданий
№ 5.1. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 4 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
1. у=ех;
2. 
;
3. у= ln x;
4. 
;
5. y= sin x;
6. y=e 2 x;
7. 
;
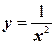8. у= (х– 1 ) 2;
9. y= cos x;
10. y =ln x 2;
№ 5.2. Получить таблицы значений следующих функций на интервале от 1 до 3 с шагом 0,2. Пользуясь безразностными формулами по 3 точкам, найти численные значения первой производной в этих точках, и сравнить полученные значения с аналитическими.
11. у =sin x;
12. y =cos x;
13. y =sin (x 2 );
14. y =sin2 x;
15. y =cos2 x;
16. y =sin ( 2 x);
17. y =cos ( 2 x);
18. 
;
19. y= ln2 x;
20. y= ln3 x;
№ 5.3. Для перечисленных функций, пользуясь безразностными формулами по 4 точкам, найти вторые производные в точках от 1 до 3 с шагом 0,2 и сравнить полученные значения с аналитическими.
21. y = e 2 x ;
22. 
;
23. 
;
24. у =(х –1)2;
25. y =ln(x 2);
26. y = 
;
27. y= sin2 x;
28. 
;
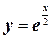29. 
;
30. 
.
5.5. Контрольные вопросы
