Пусть кривая, изображенная на рис. 2.3 является графиком функции y = f (x).
Из треугольника DMKL выразим сторону KL:
KL = tg a×Dx = f / (x) × Dx = dy
Таким образом, дифференциал функции f (x) в точке х равен приращению ординаты касательной к графику этой функции в рассматриваемой точке.
Свойства дифференциала аналогичны свойствам производной.
Дифференциал сложной функции
Пусть y = f (x), x = g (t), т.е. у – сложная функция.
Тогда
dy = f ¢(x) g ¢(t) dt = f ¢(x) dx. (2.5)
Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой-то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.
Дифференциалы высших порядков
Пусть функция y = f (x) дифференцируема на интервале (a; b). Тогда в каждой точке этого интервала определен дифференциал dу = f / (x) dx функции f (x), называемый также дифференциалом первого порядка (или первым дифференциалом).
Дифференциалом второго порядка (или вторым дифференциалом) от функции y = f (x) в точке х Î(a; b) называется дифференциал от дифференциала первого порядка функции f (x) в этой точке.
Дифференциал второго порядка обозначается d 2 f (х) или d 2 y (читается: «дэ два игрек»). Таким образом, d 2 y = d (dy). Учитывая, что dу = f / (x) dx, где dx – не зависящая от х константа получим
d 2 y = f //(x) dx 2.
Аналогично определяются дифференциалы третьего и более высоких порядков: d 3 y = d (d 2 y), d 4 y = d (d 3 y), … В общем случае, дифференциалом п-ного порядка от функции f (x) в точке x называется дифференциал от дифференциала (п –1)-го порядка функции f (x) в этой точке:
dny = d (dn–1y), где dny = f ( n ) dxn.
Отсюда следует, что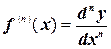 
.
Заметим, что для дифференциалов высших порядков свойство инвариантности не имеет места.
Примеры
№1. Найти производную функции 
.
Решение.
№2. Найти производную функции 
.
Решение.
№3. Точка движется по закону х (t) = t – sin t. Определить скорость и ускорение точки в момент времени t =4 с.
Решение.
Воспользуемся формулой (3.3.1):
V = х ′(t) = (t – sin t) ′ = 1 – cos t,
V (4)=1–cos 4»1,6 (м/с).
Аналогично по формуле (3.3.2):
а = V ′ = (1 – cos t) ′ = sin t,
а (4)=sin 4»–0,76 (м/с 2).
№4. Найти дифференциал функции f (x) = ln(x 2+1).
Решение.
По формуле (3.8.1) получим
df = (ln (x 2+1)) ′ dx = 
№5. Найти производную второго порядка от функции f (x) = sin2 х.
Решение.
№6. Вычислить значение дифференциала функции f (x) = х 3+2 х, когда х изменяется от 1 до 1,1.
Решение.
Прежде находим общее выражение для дифференциала этой функции:
df = (x 3 + 2 x) ′ dx = (3 x 2 + 2) dx.
Определим приращение аргумента Δx = dx = 1,1–1=0,1.
Подставляя значения dx = 0,1и x = 1в последнюю формулу, получаем искомоезначение дифференциала: df =0,5.
№7. Используя понятие дифференциала, найти приближенное значение 
.
Решение.
Рассмотрим функцию f (x) = 
. Требуется вычислить значение f (1,06). Выберем х 0 = 1, Δх = 0,06 и воспользуемся формулой (3.7.2)
f (1+0,06) ≈ f (1)+ f /(1) 0,06= 
.
Здесь мы воспользовались равенством 
Варианты заданий
№2.1. Найти производные следующих функций:
1. у = сos3 x;
2. 
;
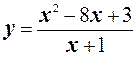3. у =(3 x +2)(x 2+4 x –1);
4. 
;
5. 
;
6. 
;
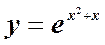7. 
;
8. 
;
9. 
;
10. 
11. 
12. 
13. 
14. у = 
15. у =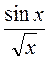 
16. 
17. 
18. 
19. у = sin3(2x + π/6)
20. y = (3x+1)2(2x-3)7
21. 
22. y = cos(sin(cos(sinx)))
23. y = x3 + ex –cos3x
24. 
25. 
26. 
27. 
28. 
29. 
30. 
31. 
32. y = xtgx
33. y = xcosx
34. y = xsin2x
35. y = 
№2.2. Найти производную данной функции в точке х 0:
1. 
;
2. 
;
3. 
;
4. 
.
№2.3. Найти производные указанных порядков для следующих функций:
1. y = ln cos x, y //=?;
2. y = 5 x, y ///=?;
3. y = sin2 x, y ///=?;
4. 
;
5. 
, у //=?;
6. 
.
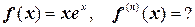№2.4. Решить следующие задачи:
1. Составить уравнение касательной к гиперболе 
в точке с абсциссой х =–0,5.
2. Точка движется по прямой так, что ее расстояние s от начального пункта через t сек. равно 
. В какие моменты точка была в начальном пункте? В какие моменты ее скорость равна нулю?
3. Количество вещества, протекшее через проводник, начиная с момента времени t =0, дается формулой Q =2 t 2+3 t +1 (кулонов). Найти силу тока в конце пятой секунды.
4. Составить уравнения касательных к линии 
в точках ее пересечения с осью абсцисс.
№2.5. Найдите производную указанной функции, сначала по х, считая t постоянной, а затем по t, считая х постоянной:
1. 
2. 
3. 
№2.6. Найти дифференциалы указанных порядков для следующих функций:
1. 
, d –?
2. 
, d –?
3. ln (ln x), d –?
4. sin 2 x, d 2–?
5. e cos x , d 2–?
6. ex + x 2, d3–?
7. 
, d –?
8. e 2 x , d (n)–?
№2.7. Вычислить приближенно:
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. ln 1,02.
Контрольные вопросы
1. Что такое приращение аргумента и приращение функции.
2. Какие значения могут они принимать?
3. Дайте определение производной функции в точке.
4. Запишите различные обозначения производной.
5. Что является биологическим смыслом производной?
6. Объясните алгебраический, физический смысл производной?
7. Объясните геометрический смысл производной.
8. Приведите примеры производной.
9. Что называется производной сложной функции?
10. Что называется производной высшего порядка?
11. Дайте понятие дифференциала функции.
12. Для всех ли функций существует дифференциал?
13. В чем состоит алгебраический смыслы дифференциала
14. В чем состоит геометрический смыслы дифференциала?
15. Докажите, что дифференциал аргумента равен его приращению.
16. Перечислите свойства дифференциала.
17. Дайте определения, в том числе в виде математического выражения, дифференциала 2-го порядка, n-го порядка.
