Рязань 2009
УДК 517.2/.3 + 519.2 (075.8)
ББК 22.161.1+22.17
М 34
Авторы – составители: М.П. Булаев, М.Н. Дмитриева, Н. В. Дорошина, И.С. Маркова, О.А. Назарова, Е.В. Прохорова
Рецензенты: С.П. Вихров, д.ф.-м.н., профессор Рязанского
государственного радиотехнического
университета;
А.Н. Пылькин, д.т.н., профессор Рязанского государственного радиотехнического университета;
|
Предназначен для первоначального изучения дифференциального и интегрального исчисления, теории вероятностей и математической статистики. Практикум рассчитан на студентов специальностей 060101, 060104, 060105, 060108, 030302 дневной, вечерней и заочной форм образования.
Он также может быть полезен студентам других гуманитарных специальностей.
УДК 517.2/.3+519.2 (075.8)
ББК 22.161.1+22.17
Табл.: 60 Ил.: 38 Библиогр.: 10 назв.
Печатается по решению Учебно-методического Совета Рязанского государственного медицинского университета.
ã ГОУ ВПО «РязГМУросздрава», 2009
Глава 1. Предел функции
Определение предела
Пусть функция f (x) определена в некоторой окрестности точки х = а (т.е. в самой точке х = а функция может быть и не определена)
Число А называется пределом функции f (x) при х ® а, если для любого e >0 существует такое число D>0, что для всех х таких, что 0 < ï x – a ï < D верно неравенство ï f (x) – A ï< e (рис. 1.1).
То же определение может быть записано в другом виде:
Если а – D < x < a + D, x ¹ a, то верно неравенство А – e < f (x) < A + e.
Запись предела функции в точке: 
.
Если f (x) ® A 1 при х ® а только при x < a, то 
называется пределом функции f (x) в точке х = а слева, а если f (x) ® A 2 при х ® а только при x > a, то 
называется пределом функции f (x) в точке х = а справа (рис. 1.2).
Приведенное выше определение относится к случаю, когда функция f (x) не определена в самой точке х = а, но определена в некоторой сколь угодно малой окрестности этой точки.
Пределы А 1 и А 2 называются также односторонними
пределами функции f (x) в точке х = а. Также говорят, что А – конечный предел функции f (x).
Операции над пределами
1. Предел постоянной есть сама постоянная: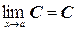 
, где С = const.
Следующие свойства справедливы при предположении, что функции f (x) и g (x) имеют конечные пределы при х ® а;
2. Предел суммы (разности) равен сумме (разности) пределов:
;
3. Предел произведения равен произведению пределов:
;
4. Постоянную можно выносить за знак предела:
;
5. Предел отношения равен отношению пределов:
, при 
;
6. Если f (x)> 0 вблизи точки х = а и , то А >0.
Аналогично определяется знак предела при f (x) < 0, f (x) ³ 0, f (x) £ 0;
7. Если g (x) £ f (x) £ u (x) вблизи точки х = а и 
, то и 
;
8. 
;
9. 
;
10. 
;
11. 
;
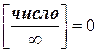12. Неопределенность вида 
можно раскрыть, если числитель и знаменатель дроби разделить на высшую степень переменной;
13. Неопределенность вида 
можно раскрыть, если числитель и знаменатель дроби разложить на множители и сократить.
Замечательные пределы
Найдем предел отношения двух многочленов, т.е. 
, где
P (x) = a 0 xn + a 1 xn– 1 +…+an, Q (x) = b 0 xm + b 1 xm– 1 +…+bm. Преобразуем данную дробь следующим образом
Таким образом, 
Первый замечательный предел: 
Второй замечательный предел: 
, где е постоянная, которая приблизительно равна 2,718281828…
Часто если непосредственное нахождение предела какой-либо функции представляется сложным, то можно путем преобразования функции свести задачу к нахождению замечательных пределов.
Кроме трех, изложенных выше, пределов можно записать следующие полезные на практике соотношения:
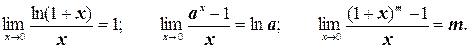
При решении многих задач используются следующие эквивалентности, верные при х ®0:
1. 
~ х;
2. 1–cos x ~ 
;
3. tg x ~ x;
4. arcsin x ~ x;
5. arctg x ~ x;
6. ln (1+ x) ~ x;
7. ax –1 ~ x ln a;
8. 
~ 
.
Примеры
№1. Используя свойства пределов функций, найти следующие пределы:
а)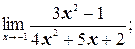 
б) 
в) 
г)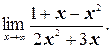 
Решение.
а) Применяя теорему о действиях над пределами функций, получим:
б) Так как пределы числителя и знаменателя при х ®2 равны нулю, то мы имеем неопределенность вида 
. «Раскроем» эту неопределенность (т.е. избавимся от нее), разложив числитель и знаменатель на множители и сократив их далее на общий множитель х– 2:
.
в) Здесь мы также имеем неопределенность вида . Домножим числитель и знаменатель дроби на выражение, сопряженное к числителю (избавимся от иррациональности в числителе):
г) Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь имеет место неопределенность вида 
. Раскроем эту неопределенность. Поделим числитель и знаменатель дроби на высшую степень х, т.е. на х 2:
Таким образом,
№2. Найти пределы:
а) 
б) 
в) 
г)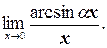 
Решение.
а) Сделаем замену у=αх; тогда у ®0 при х ®0 и 
. В последнем равенстве мы воспользовались первым замечательным пределом. Таким образом, 
б) Поделим числитель и знаменатель дроби под знаком предела на х, после чего воспользуемся предыдущим пунктом:
в) Сводя предел к первому замечательному пределу, сделаем замену у = х – 
. Тогда у ®0 при х ® , а х = у + , откуда:
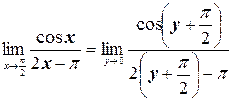
Во втором равенстве в этой цепочке мы использовали формулу приведения, а в последнем – первый замечательный предел.
г) Так как х ®0, то воспользуемся эквивалентностью №4:
.
Варианты заданий
№1.1. Найти пределы:
а) 
;
б) 
;
в) 
;
г) 
;
д) 
;
е) 
;
ж) 
;
з) 
;
и) 
;
к) 
;
л) 
;
м) 
.
№1.2. Найти пределы:
а) 
;
б)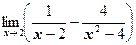 
;
в) 
;
г) 
;
д) 
;
е) 
;
ж) 
;
з)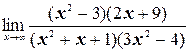 
;
и) 
;
к)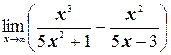 
.
№1.3. Найти пределы:
а) 
;
б) 
;
в) 
;
г)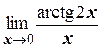 
;
д) 
;
е) 
;
ж) 
;
з) 
Контрольные вопросы
Глава 2. Производная и дифференциал
Понятие производной
Рассмотрим функцию y = f (x). Предположим, что x 0 внутренняя точка множества определения функции. Зададим приращение аргумента D x ¹0 такое, что точка x 0+D x Î Df. Тогда соответствующее приращение в т. x 0 будет иметь вид: Df = f (x 0+D x)– f (x 0).
Если существует предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента D х ®0, то он называется значением производной функции f (x) в точке х 0
Обозначение: 
.
Также возможны и другие обозначения: 
, 
.
Если функция y = f (x) имеет конечную производную в каждой точке некоторого промежутка, то производную можно считать функцией переменной х и обозначать у /(х), 
.
Если в точке x 0 существует конечная производная функции y = f (x), то эта функция называется дифференцируемой в точке x 0.
Если функция y = f (x) дифференцируема в каждой точке некоторого промежутка, то она дифференцируема на промежутке.
