Экономический прогноз – это система научных исследований о возможных направлениях будущего развития экономики и отдельных ее сфер.
Прогнозирование означает специальные научные исследования конкретных перспектив развития какого-либо явления и находится во взаимосвязи с планированием, программированием и управлением.
Прогнозирование для отдельного объекта исследования или отдельного предприятия означает процесс формирования прогнозов его развития на основе предыдущих тенденций развития, изменяющихся во времени, т.е. показателей рядов динамики.
Распространение установленных в прошлом тенденций на будущий период или нахождение значений признака за пределами анализируемого периода называется экстраполяцией.
Экстраполяция, проводимая в будущее, называется перспективной, а в прошлое – ретроспективной.
Применение экстраполяции для прогнозирования должно основываться на предположении, что найденная закономерность развития внутри динамического ряда сохраняется и вне этого ряда.
Это означает, что основные факторы, сформировавшие выявленную закономерность изменения уровней ряда во времени, сохранятся и в будущем.
Возможность распространения тенденции как в будущее, так и в прошлое заложена в свойстве массовых явлений и процессов, называемой инерционностью. То есть, если массовое явление или процесс обладают определенным свойством, то они теряют или изменяют это свойство не мгновенно, а постепенно и не сразу.
Экстраполяция в прогнозировании базируется на двух основных предпосылках:
· развитие описывается плавной кривой;
· общая тенденция развития в прошлом и настоящем не претерпевает серьезных изменений.
Существует экстраполяция во времени и в пространстве.
Экстраполяция во времени применяется для перспективных расчетов показателей динамики в различных областях знаний.
Экстраполяция в пространстве – это распространение выборочных данных на другую часть совокупности, не подвергнутую наблюдению.
Чем короче срок экстраполяции (период упреждения), тем более надежные и точные результаты дает прогноз. В зависимости от того, какие принципы и исходные данные положены в основу прогноза, выделяют следующие методы экстраполяции:
· среднего абсолютного прироста;
· среднего темпа роста;
· выравнивания по аналитической формуле.
Эти способы экстраполяции тренда являются самыми приближенными.
Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если есть уверенность считать общую тенденцию линейной.
Если основная тенденция изменений признака близка к прямолинейной, то значение уровня ряда в последующий период (n +1) можно приблизительно определить по формуле:
 , где:
, где:
 - средний абсолютный прирост.
- средний абсолютный прирост.
Период учреждения прогноза (L) не должен превышать 1/3 n, т.е.
L‹1/3 п, где:
п - число членов анализируемого динамического ряда.
Прогнозирование по среднему темпу роста осуществляется в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспоненциальной) кривой. В этом случае экстраполяция осуществляется по формуле:
 , где
, где
y n – последний уровень ряда динамики;
t – срок прогноза;
 – средний коэффициент роста.
– средний коэффициент роста.
Наиболее распространенным методом прогнозирования считают аналитическое выражение тренда.
Нахождение по имеющимся данным за определенный период времени некоторых недостающих значений признака внутри исследуемого периода называется интерполяцией.
Как и экстраполяция, интерполяция может производиться на основе среднего абсолютного прироста, среднего темпа роста и с помощью аналитического выравнивания.
При составлении прогнозов уровней социально-экономических явлений обычно оперируют интервальной оценкой, рассчитывая так называемые доверительные интервалы прогноза.
Решение типовых задач
7.6.1. Постройте модель, описывающую динамику процесса производства легковых автомобилей в РФ (тыс. шт.) и постройте линию тренда:
| месяц | выпуск легковых автомобилей, тыс.шт.(у) |
| 87,2 | |
| 81,0 | |
| 82,4 | |
| 85,8 | |
| 90,4 | |
| 84,0 | |
| 96,3 | |
| 85,5 | |
| 83,0 | |
| итого | 775,6 |
Решение:
1. Аналитически модель линейного тренда выражается следующим уравнением прямой линии: 
2. подбираем функцию для описания ряда с условием  ;
;
3. для нахождения значений параметров а 0 и а 1 системы уравнений необходимо сделать дополнительные расчеты и найти  и
и  .
.
Результаты запишем в таблицу:
| месяц | у | t | 
| 
| 
|
| 87,2 | -4 | -348,8 | 84,7 | ||
| 81,0 | -3 | -243,0 | 85,1 | ||
| 82,4 | -2 | -164,8 | 85,5 | ||
| 85,8 | -1 | -85,8 | 85,8 | ||
| 90,4 | 86,2 | ||||
| 84,0 | 84,0 | 86,5 | |||
| 96,3 | 192,6 | 86,9 | |||
| 85,5 | 256,5 | 87,3 | |||
| 83,0 | 87,6 | ||||
| ∑ | 775,6 | 22,7 | 775,6 |
4. находим значения параметров а 0 и а1 трендовой модели:




5. модель динамики производства легковых автомобилей:

6. подставляем имеющиеся в условии помесячные значения t и получаем средние помесячные уровни выпуска автомобилей:


……………………………………….
7. проверим правило средних величин:
Сумма расчетного  должна быть равна сумме исходных
должна быть равна сумме исходных  :
:


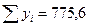
Правило выполнено, значит модель построена и вычислена верно;
8. построим линию тренда в осях координат:
· сначала нанесем линию фактической динамики;
· затем нанесем линию средних значений динамики по месяцам и получим линейный тренд, выровненный методом наименьших квадратов;
· далее можно построить прогноз на будущее графически продлением линии тренда, т.к. 


и аналитически: 

7.6.2. Требуется провести анализ динамики продажи мясных консервов за 2006-2010 г.г. по условным данным, т.е. определить абсолютные приросты (Δ у), темпы роста или снижения продажи мясных консервов (Тр), темпы прироста
(Δ Т), абсолютное значение 1% прироста (А1%), темпы наращивания (Тнаращ.), а также средние показатели ( ).
).
Для удобства и наглядности исходные и рассчитанные показатели изложим в одной таблице:
| год | кон- сервы мяс- ные, млн. усл. банок | абсолютные приросты (снижение), млн. усл. банок | темпы роста, % | темпы прироста, % | абсо- лютное значе- ние 1% при- роста, млн. усл. банок | темпы нара- щива-ния, % | |||
| с преды- дущим годом | с 2006 г. | с преды- дущим годом | с 2006 г. | с преды- дущим годом | с 2006 г. | ||||
| А | |||||||||
| - | - | - | 100,0 | - | 0,0 | - | - | ||
| -85 | -85 | 90,5 | 90,5 | -9,5 | -9,5 | 8,91 | -9,5 | ||
| +789 | +704 | 197,9 | 179,0 | 97,9 | 79,0 | 8,06 | 88,6 | ||
| +42 | +746 | 102,63 | 183,7 | 2,63 | 83,7 | 15,95 | 4,71 | ||
| +14 | +760 | 100,85 | 185,3 | 0,85 | 85,3 | 16,37 | 1,57 | ||
| Итого | +760 | - | - | - | - | - | - | 85,3 |
Решение:
Для определения абсолютной скорости роста (снижения) продажи мясных консервов определяем абсолютные приросты ряда динамики по формулам:
 у
у  = у
= у  - у
- у  ,
,
 у
у  = у
= у  - у
- у 
Абсолютное уменьшение продажи консервов за 2007 г. по сравнению с 2006 г. составило: 806-891 = -85 млн. усл. банок, а в 2010 году по сравнению с базисным 2006 годом продажа консервов возросла на 760 млн. усл. банок.
Интенсивность изменения уровней ряда динамики оценивается относительным показателем - темпом роста (Тр), который определяется по следующим формулам:
 ;
; 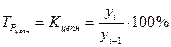 .
.
Так, для 2010 года темп роста по сравнению с 2006 годом составил:
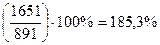 (графа 5 таблицы)
(графа 5 таблицы)
Для выражения изменения величины абсолютного прироста уровней ряда определяем темпы прироста базисные и цепные (графы 5 и 6) таблицы:
 =
= 

Например, в 2010 году продажа консервов возросла по сравнению с 2006 годом на 85,3% ( или 185,3 – 100 = 85,3%).
или 185,3 – 100 = 85,3%).
Показатель абсолютного значения прироста продажи консервов определяется по следующим формулам:

Для 2010 года абсолютное значение 1% прироста (графа 8 таблицы) равно:
 млн.усл.банок или
млн.усл.банок или  млн.усл.банок.
млн.усл.банок.
Для определения темпов наращивания продажи мясных консервов используем следующие формулы (графа 9 таблицы):

Так, например в 2007 году по сравнению с 2006 годом наблюдалось уменьшение продажи мясных консервов на 9,5%, а в 2008 году по сравнению с 2006 годом продажа консервов увеличилась на 88,6%, в 2010 году по сравнению с 2006 годом продажа консервов предприятиями потребительской кооперации увеличилась лишь на 1,57%.
Средний абсолютный прирост определяем по формуле:
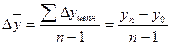
 =
=  млн.усл.банок.
млн.усл.банок.
Среднегодовой темп роста определяем по следующей формуле:
 =
=  или 116,7%.
или 116,7%.
Среднегодовой темп прироста получим, вычтя из среднегодового темпа роста 100%:
116,7% - 100% = 16,7%.
Следовательно, среднегодовой темп прироста продажи мясных консервов предприятиями потребительской кооперации региона составляет 16,7%
7.6.3. По данным о розничном товарообороте предприятия по кварталам 2009-2010 гг. произведите анализ основной тенденции развития товарооборота за указанный период времени и рассчитайте прогноз розничного товарооборота предприятия на ближайшую перспективу, т.е. определите вероятные значения розничного товарооборота на II, III и IV кварталы 2010 г. (в таблице, в графах 2-3 уже сделаны некоторые необходимые вычисления):
| показатели | розничный товарооборот, млн.руб. | темп роста, цепной, % | абсолютный прирост, цепной, млн. руб. |
| А | |||
| I кв-л 2009 г. | 694,8 | - | - |
| II кв-л 2009 г. | 753,0 | 108,4 | 58,2 |
| III кв-л 2009 г. | 1147,3 | 152,4 | 394,3 |
| IV кв-л 2009 г. | 1552,7 | 135,3 | 405,4 |
| I кв-л 2010 г | 1517,0 | 97,7 | -35,7 |
| В среднем | 1133,0 | 115,0 | 205,6 |
Решение:
Для определения основной тенденции изменения товарооборота исчислим темпы роста по годам, свидетельствующие об интенсивности развития товарооборота по кварталам, и абсолютные приросты по годам по следующим формулам:
 ,
,  ,
, 
 ,
,  .
.
Чтобы установить тип развития явления, определяющим фактором (признаком) берется характер изменения абсолютных приростов.
Абсолютные приросты стабильны, кроме последнего периода –
I квартала 2010 года. При среднем абсолютном приросте, равном 205,6 млн. руб., величина изменений абсолютных приростов колеблется и составляет
+/-29,9 млн. руб. ( ), т.е. является незначительной. Поэтому для упрощения расчетов и интерпретации полученных результатов анализируемый ряд динамики будем считать с равномерным развитием, пренебрегая последним результатом и применяя для аналитического выравнивания уравнение прямой линии.
), т.е. является незначительной. Поэтому для упрощения расчетов и интерпретации полученных результатов анализируемый ряд динамики будем считать с равномерным развитием, пренебрегая последним результатом и применяя для аналитического выравнивания уравнение прямой линии.
Для этой же цели обоснования выбора уравнения на основании данных первых двух граф табличных данных построим график зависимости розничного товарооборота от времени:

|
На основании графика можно сделать вывод в основном о прямой линейной зависимости между розничным товарооборотом и временем, т.е. выраженной уравнением прямой линии:

Для вычисления параметров уравнения способом наименьших квадратов
запишем систему нормальных уравнений:

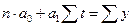 ,
,
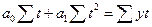 .
.
Для решения системы нормальных уравнений составим таблицу:
| кварталы | розничный товарооборот, млн. руб., (у) | условные обозначения времени, (t) | t 
| tу | теоретические уровни, ( ) )
|
| А | |||||
| I 2009 г. | 694,8 | 694,8 | 643,65 | ||
| II 2009 г. | 753,0 | 1506,0 | 888,31 | ||
| III 2009 г. | 1147,3 | 3441,9 | 1132,96 | ||
| IV 2009 г. | 1552,7 | 6210,8 | 1377,61 | ||
| I 2010 г. | 1517,0 | 7585,0 | 1622,67 | ||
| Итого: | 5664,8 | 19438,5 | 5664,80 |
Подставляя значения расчетной таблицы, определяем параметры уравнения прямолинейной функции:



 Делим каждое уравнение на коэффициенты при а
Делим каждое уравнение на коэффициенты при а  : каждый член первого уравнения делим на 5, а каждый член второго уравнения делим на 15 и получаем:
: каждый член первого уравнения делим на 5, а каждый член второго уравнения делим на 15 и получаем:

 .
.
Из второго уравнения вычитаем первое и находим параметр а  :
:
0,6666 а  = 162,94,
= 162,94,
отсюда
а  =
=  = 244,65.
= 244,65.
Значение а  подставляем в первое уравнение и находим а
подставляем в первое уравнение и находим а  :
:



а  = 398,99.
= 398,99.
Зная значения а  и а
и а  , запишем уравнение прямой линии:
, запишем уравнение прямой линии:

На основании полученного уравнения рассчитаем теоретические уровни, т.е. объемы розничного товарооборота, вычисленные по уравнению прямой, за все кварталы 2005 г. и I квартал 2006 г.
Решаем уравнение связи пять раз, подставляя вместо t имеющиеся условные значения времени.
Для I квартала 2009 г.:
( ) = 398,99 + 244,65*1 = 643,65 млн. руб.
) = 398,99 + 244,65*1 = 643,65 млн. руб.
Для второго квартала 2009 г.:
( ) = 398,99 + 244,65*2 = 888,31 млн.руб.
) = 398,99 + 244,65*2 = 888,31 млн.руб.
и т.д. (графа 5 расчетной таблицы).
Для того, чтобы сделать прогноз розничного товарооборота на II, III и IV кварталы 2010 года, необходимо в данное уравнение подставить следующие значения времени:
для II квартала 2010 г. t = 6;
для III квартала 2010 г. t = 7;
для IV квартала 2010 г. t = 8.
Произведя все расчеты, находим прогноз товарооборота на II квартал 2010 г.:
 = 398,99+244,65*6 = 18866,92 млн. руб.;
= 398,99+244,65*6 = 18866,92 млн. руб.;
III квартал 2010 г.– 2111,58 млн.руб.; IV квартал 2010 г.– 2356,23 млн. руб.
Эта модель будет действительна при условии, что в дальнейшем сохранится та же тенденция развития данного экономического явления, каким является закономерность формирования розничного товарооборота имеющегося предприятия.
В полученном уравнении прямой линии ао является свободным членом и показывает то значение товарооборота, начиная с которого выполняется имеющаяся закономерность изменения товарооборота. Наибольшее значение имеет коэффициент регрессии а1 , который показывает, что при изменении времени на одну условную единицу (квартал) розничный товарооборот возрастает в среднем за квартал на 244,65 млн.рублей.
7.6.4. Реализация кондитерских изделий в магазинах области характеризуется следующими данными:
| месяц | год | ||
| Январь | 131,8 | 132,1 | 137,3 |
| Февраль | 127,9 | 130,8 | 132,2 |
| Март | 128,9 | 133,0 | 142,0 |
| Апрель | 139,5 | 135,8 | 140,9 |
| Май | 136,2 | 129,1 | 136,8 |
| Июнь | 141,4 | 130,9 | 140,3 |
| Июль | 139,4 | 131,4 | 135,3 |
| Август | 134,3 | 129,3 | 134,0 |
| Сентябрь | 134,7 | 132,5 | 133,7 |
| Октябрь | 134,6 | 135,6 | 134,9 |
| Ноябрь | 136,3 | 134,7 | 135,3 |
| Декабрь | 141,6 | 138,2 | 142,7 |
| Итого | 1626,6 | 1593,4 | 1645,4 |
На основе проведенных данных:
1) определите характер общей тенденции динамики реализации кондитерских изделий;
2) применяя соответствующую формулу индекса сезонности, измерьте сезонные колебания реализации кондитерских изделий;
3) показатели сезонной волны изобразите графически;
4) на основе синтезированной модели сезонной волны сделайте прогноз объемов реализации по месяцам 2005 года возможного поступления в магазины 1700 тонн кондитерских изделий.
Решение:
Определим характер общей тенденции ряда динамики реализации кондитерских изделий:
Таблица А
| год | среднемесячный уровень, тонн | базисные темпы роста, % |
| 1626,6:12=135,55 | ||
| 1593,4:12=132,78 | 97,95 | |
| 1645,4:12=137,12 | 101,15 |
Определенной закономерности здесь не выявляется, так как на основании базисных темпов роста можно сказать, что реализация кондитерских изделий в 2009 г. по сравнению с 2008 г. падает на 2,05% (97,95%-100%), а в 2010 г. по сравнению с 2009 г. возрастает на 1,15% (101,15%-100%).
Показатель среднегодового темпа роста также свидетельствует об отсутствии значительной тенденции роста, исчисленный по следующей формуле:
 или 100,57%.
или 100,57%.
Средний темп прироста 

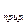 =0,57%.
=0,57%.
Основная тенденция развития непосредственно не просматривается.
Следовательно, для дальнейшего решения суммируются данные по месяцам за три года  (из таблицы А):
(из таблицы А):
для января 131,8+132,1+137,3=401,2
для февраля 127,9+130,8+132,2=390,9
для марта 128,9+133,0+142,0=403,9
и т.д.
Затем по формуле простой средней арифметической  =
=  , которая является постоянной для каждого месяца, находим среднее значение
, которая является постоянной для каждого месяца, находим среднее значение  реализации кондитерских изделий за каждый месяц в среднем за три года:
реализации кондитерских изделий за каждый месяц в среднем за три года:
для января 
 =
=  =133,73 тонн
=133,73 тонн
для февраля  февр =
февр =  130,30 тонн и т.д.
130,30 тонн и т.д.
Для каждого месяца эти значения определены в графе 2 таблицы Б.
В последней строке графы 1 определен знаменатель формулы индекса сезонности в виде общего для всего ряда динамики среднего уровня  , также по формуле средней арифметической простой:
, также по формуле средней арифметической простой:

 тонн
тонн
Таблица Б
| месяцы | всего за 3 года, тонн

| в среднем за 3 года, тонн
 = =  
| индекс сезонности, %
I  = ( = ( : :  )* 100% )* 100%
| прогноз на
2007 г., тонн
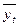
|
| А | ||||
| Январь | 401,2 | 133,73 | 99,0 | 141,7*0,99=140,3 |
| Февраль | 390,9 | 130,30 | 96,4 | 136,6 |
| Март | 403,9 | 134,63 | 99,6 | 141,1 |
| Апрель | 416,2 | 138,73 | 102,7 | 145,5 |
| Май | 402,1 | 134,03 | 99,2 | 140,6 |
| Июнь | 412,6 | 137,53 | 101,8 | 144,3 |
| Июль | 406,1 | 135,37 | 101,2 | 143,4 |
| Август | 397,6 | 132,53 | 98,1 | 139,0 |
| Сентябрь | 400,9 | 133,63 | 98,9 | 140,1 |
| Октябрь | 405,1 | 135,03 | 99,9 | 141,6 |
| Ноябрь | 406,3 | 135,43 | 100,2 | 142,0 |
| Декабрь | 422,5 | 140,83 | 104,2 | 147,7 |
| Итого | 4865,4 | 1621,77 | 100,0 | 1700,0 |
Этот общий средний уровень ( ) и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, которые помещены в графе 3 таблицы 3:
) и используется в качестве постоянной базы сравнения при определении средних индексов сезонности, которые помещены в графе 3 таблицы 3:

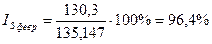 и т.д.
и т.д.
Из графы 3 таблицы 3 видно, что сезонные колебания реализации кондитерских изделий характеризуются повышением реализации в декабре (+4,2%), апреле (+2,7%), июне (+1,8), июле (+1,2), ноябре (+0,2) и снижены в других месяцах.
Характер сезонных колебаний покажем на графике сезонной волны реализации кондитерских изделий в магазинах области в 2008-2010 годах по месяцам (в % к среднему уровню, который составляет 100%):
 
|
На графике видно, что наибольшая реализация кондитерских изделий приходится на апрель, июнь, июль, ноябрь и декабрь, а наименьшая реализация – на февраль и август, что подтверждает выполненные аналитические расчеты.
Эта же тенденция в реализации кондитерских изделий сохранится и на предстоящий период, т.е. на 2011 год.
Мерой сезонной колеблемости является среднее квадратическое отклонение (σ), расчет которого произведен в таблице В:
Таблица В
| месяц | в среднем за 3 года, тонн ( ) )
| отклонение от среднего, тонн
  - - 
| квадрат отклонения

|
| январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь | 133,7 130,3 134,6 138,7 134,0 137,5 135,4 132,5 133,6 135,0 135,4 140,8 | -1,3 -4,7 -0,4 +3,7 -1,0 +2,5 +0,4 -2,5 -1,4 +0,4 +5,8 | 1,69 22,09 0,16 13,69 1,00 6,25 0,16 6,25 1,96 0,16 33,64 |
| итого | 1621,77 | - | 87,05 |
| в среднем | 135,14 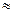 135,0 135,0
| - | 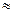 7,25 7,25
|
 тонн.
тонн.
Коэффициент сезонной колеблемости (VS) определяется по формуле:

На основе значений сезонной волны по месяцам сделаем прогноз поступления в магазин кондитерских изделий по месяцам 2011 года, если общий объем реализации за весь год составит 1700 тонн.
Для этого найдем сначала средний месячный объем реализации:
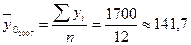 тонн.
тонн.
Чтобы определить или дать прогноз объемов реализации кондитерских изделий на каждый месяц, необходимо полученную сумму 141,7 тонн умножить на значения соответствующих индексов сезонности для каждого месяца:
для января - 141,7 * 0,99 = 140,3 т;
для февраля - 141,7 * 0,964 = 136,6 т
и т.д.
Указанные расчеты помещены в графе 4 таблицы Б, причем общая сумма реализации за все 12 месяцев равна исходной сумме 1700 тонн, что свидетельствует о правильности проведенных расчетов.






