При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы, такие как укрупнение интервалов, метод скользящей средней и аналитическое выравнивание.
В основу этих методов положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития явления выражается в виде некоторой плавной линии.
7.2.1. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда и определение итога уровня для этих интервалов (по интервальным рядам абсолютных величин) или исчисление средних для каждого укрупненного интервала.
При использовании переменной средней укрупнение интервалов обычно начинают с объединения двух периодов. Если же тенденция четко не проявляется, переходят к объединению трех периодов и т.д.
Недостатком этого метода является то, что из поля зрения выпадает процесс изменения внутри укрупненного интервала, что вызвано сокращением числа уровней изучаемого ряда.
Однако преимуществом данного метода является сохранение экономической природы явления.
Расчет переменной средней осуществляется по формулам средней арифметической простой (объединение трех периодов):
; 
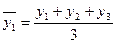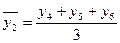и т.д., где:
у1, у2, у3 …..уп - уровни исходного ряда динамики.
7.2.2. Метод скользящей средней основан на замене абсолютных показателей ряда динамики средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего:
; 
; 
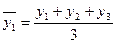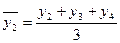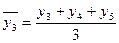и т.д.
Полученные средние записываются к соответствующему срединному интервалу (второму, третьему, четвертому и т.д.).
Обеспечиваемое при применении метода скользящей средней погашение колебаний величин индивидуальных уровней ряда динамики называется сглаживанием динамического ряда.
Недостатком этого метода является то, что сглаженный ряд «укорачивается», т.е. происходит потеря информации по сравнению с фактическим на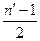 
члена ряда с одного и другого конца,
где:
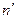- количество уровней, входящих в новый интервал.
Вместе с тем, чем продолжительнее интервал сглаживания, тем сильнее усреднение, а потому выявляемая тенденция развития получается более плавной.
7.2.3. Метод аналитического выравнивания является наиболее эффективным способом выявления основной тенденции развития явлений и позволяет получить количественную модель, выражающую общую тенденцию изменения уровней динамического ряда во времени. В этом случае фактические уровни заменяются уровнями, вычисленными на основе определенной прямой или кривой, выбранной в предположении, что она отражает общую тенденцию изменения во времени изучаемого явления. При этом уровни ряда динамики выражаются в виде функции времени:
.
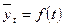Тенденцию ряда динамики, представленную в виде гладкой кривой, аналитически выраженной функцией времени, называют трендом f(t).
Тренд характеризует основную закономерность движения во времени, свободную в основном (но не полностью) от случайных воздействий.
Уровни временного ряда описывают следующим уравнением тренда:
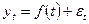, где:
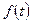— систематическая составляющая, характеризующая основную тенденцию;
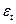— случайная составляющая.
Логический анализ при выборе вида уравнения может быть основан на рассчитанных показателях динамики, а именно:
· если относительно стабильны абсолютные приросты (первые разности уровней приблизительно равны), сглаживание может быть выполнено по прямой;
· если абсолютные приросты равномерно увеличиваются (вторые разности уровней приблизительно равны), можно принять параболу второго порядка;
· при ускоренно возрастающих (замедляющихся) абсолютных приростах принимают параболу третьего порядка;
· при относительно стабильных темпах роста принимают показательную функцию.
В зависимости от вида функции различают следующие основные формы тренда:
1) Линейная модель: 
, где:
у — уровни, освобожденные от колебаний, выровненные по прямой;
a0 — начальный уровень тренда в момент или период, принятый за начало отсчета времени;
a1 — среднегодовой абсолютный прирост (среднее изменение за единицу времени t, константа тренда.
Линейный тренд хорошо отражает тенденцию изменений при действии множества разнообразных факторов, изменяющихся различным образом по разным закономерностям.
2) Показательная модель: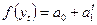 
, где:
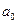- уровень ряда за период (в момент) времени t=0;
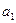- средний коэффициент роста за единичный промежуток времени.
3) Параболическая модель: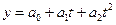 
, где:
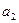- квадратический параметр, равный половине ускорения, константа параболического тренда.
Параболическая форма тренда выражает ускоренное или замедленное изменение уровней ряда с постоянным ускорением. Такой характер развития можно ожидать при наличии важных факторов прогрессивного (регрессивного) развития.
4) Логарифмическая модель: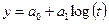 
Логарифмический тренд пригоден для отображения тенденции замедляющегося роста уровней при отсутствии предельно-возможного значения.
