Сущность выборочного наблюдения – определить пределы генеральной средней величины (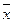
) или генеральной доли (Р).
· для количественного признака сущность раскрывается в следующей формуле:
,
которая определяет пределы генеральной средней величины 
.
· для качественного признака пределы генеральной доли (удельного веса) определяются по формуле:
P = w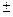 
Dw
6.5. Расчет необходимого объема выборки
Так как величина ошибки выборки зависит от численности выборочной совокупности n, при подготовке выборочного наблюдения возникает задача определения необходимой численности собственно-случайной выборки – такой, которая обеспечит заданную точность результатов исследования.
6.5.1. При повторном отборе необходимая численность выборки определяется по формулам:
| - при оценивании объема выборки для количественных совокупностей |
- при оценивании выборочной доли для качественных совокупностей, т.к. 
|
6.5.2. При бесповторном отборе необходимая численность выборки определяется по формулам:
- при оценивании среднего значения выборки;
- при оценивании выборочной доли.
Полученный на основе использования этих формул результат всегда округляется в большую сторону до целого значения.
Малая выборка
В практике статистических исследований массовых процессов и явлений часто приходится сталкиваться с небольшими по объему выборками, которые так и называются – «малые выборки».
Малая выборка – это такое выборочное наблюдение, численность единиц которого не превышает 30.
Малая выборка в настоящее время используется более широко, чем раньше, за счет того, что на ее организацию требуется гораздо меньше временных, материальных и трудовых затрат, чем на сплошное статистическое обследование. Кроме того, в настоящее время появляется все большее количество новых форм массовых явлений и процессов (в основном связанных с развитием рыночных отношений в экономике), число которых позволяет говорить об их немногочисленности, иногда единичности. Поэтому, иногда приходится ограничиваться малым числом наблюдений.
При оценке результатов малой выборки для определения возможных пределов ошибки используется критерий Стьюдента, определяемый по формуле:
, где
-мера случайных колебаний выборочной средней в малой выборке,
t – коэффициент доверия, затабулированный в специальных таблицах Стьюдента.
Расчет ошибок в малой выборке мало отличается от аналогичных вычислений в большой выборке. Правда, в малой выборке вероятность будет немного меньше, чем в большой; и точность результатов выборки малого объема все же ниже, чем при большой выборке.
Решение типовых задач
6.7.1. Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали.
Результаты выборки следующие:
| вес, мг | 38-40 | 40-42 | 42-44 | 44-46 |
| число спиралей |
Определитес вероятностью λ = 0,95 (при этом определяем по таблице, что коэффициент доверия t = 1,96 ) доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.
Решение:
Доверительные интервалы для генеральной средней с вероятностью λ:
, где:
- средний уровень признака по выборке.
мг
Δx = 
t = t 
По условию задачи 
или 0,2, следовательно N = 
шт.
мг.
Определяем доверительные интервалы для генеральной средней с вероятностью λ = 0,95:
или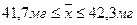 
6.7.2. В микрорайоне проживает 5000 семей. В порядке случайной бесповторной выборки предполагается определить средний размер семьи при условии, что ошибка выборочной средней не должна превышать 0,8 человека с вероятностью λ = 0,954 и при среднем квадратическом отклонении 3,0 человека.
Решение.
Так как при λ = 0,954 t=2, то в этом случае необходимая численность выборки равна:
= 
семей
6.7.3. На заводе электроламп из партии продукции в количестве 16 000 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными.
Определитес вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.
Решение:
1.Определяем долю бракованной продукции в выборке:
или 2,5%
2.При вероятности 
t = 3,0 (находим по таблице)
3.Размер предельной ошибки:
или 1,1%.
4.Доверительные интервалы для генеральной доли с вероятностью определяем по формуле:
следовательно: 
или 
Можно сказать с вероятностью l = 0,997, что во всей партии продукции процент брака будет находиться в пределах от 1,4% до 3,6%.
6.7.4. На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.
Определитечисленность выборки, и результаты выборки дайте с точностью до 1% и гарантией этого с вероятностью λ =0,95, при доле выборки = 0,5 (
= 0,5).
Решение:
По условию задачи известны:
Размер допустимой (предельной) ошибки -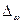 
= 1%, или 0,01;
принятая вероятность – λ = 0,95;
при λ = 0,95 t (коэффициент доверия) = 1,96.
Необходимая численность выборки:
n = 
= 9604.
Таким образом, чтобы с заданной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.
6.7.5. По городской телефонной сети в порядке случайной выборки (механический отбор) произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора - 5 минут при среднеквадратическом отклонении 2 минуты.
Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 секунд?
Решение:
По условию задачи известно:
Объем выборки – n =100;
Выборочная средняя =5 мин.
Выборочное среднеквадратическое отклонение σ = 2 мин.;
Предельная ошибка выборки - 
,
Следовательно, согласно имеющимся формулам:
t = 
Затем по таблице значений «t» на основе полученного в результате вычислений t определяем вероятность того, что ошибка не превысит заданной величины: при t = 1,5 вероятность λ = 0,866.
Следовательно, с вероятностью λ = 0,866 можно утверждать, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 секунд.
6.7.6. Необходимо провести социологическое исследование с вероятностью 95,4% (λ = 0,954), посвященное опознанию потребителями торговой марки. Предельно допустимая ошибка данного исследования не должна превышать 5%. Какое количество респондентов необходимо опросить в порядке собственно случайной повторной выборки для решения данной проблемы?
Решение:
Следовательно, обследованию необходимо подвергнуть не менее 400 респондентов не предмет узнаваемости торговой марки компании.
