| стаж работы, лет | число продавцов, чел.(f) | середина интервала
(x  )
| отклонение варианты от
средней ( )
| 
| 
|
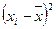
| 0-3 | 1,5 | -5,0 | 25,0 | 150,0 | |
| 3-6 | 4,5 | -2,0 | 4,0 | 28,0 | |
| 6-9 | 7,5 | +1,0 | 1,0 | 10,0 | |
| 9-12 | 10,5 | +4,0 | 16,0 | 80,0 | |
| 12-15 | 13,5 | +7,0 | 49,0 | 98,0 | |
| Итого: | - | - | - | 366,0 |
Вычисляем средний стаж работы:
= 
= 
= 
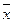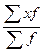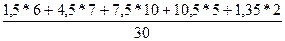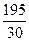= 6,5 лет
Вычисляем дисперсию:
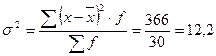
Следует иметь в виду, что дисперсия – безмерная величина и самостоятельного экономического значения не имеет. Дисперсия необходима для расчета среднего квадратического отклонения. В данном случае среднее квадратическое отклонение равно:
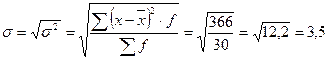года.
Среднее квадратическое отклонение показывает, что в среднем варианты
отклоняются от средней арифметической (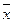 = 6,5) на 3,5 года при колеблемости стажа работы отдельных работников от 0 до 15 лет.
Для характеристики степени колеблемости признака необходимо среднее квадратическое отклонение выразить в процентах к средней арифметической, т.е. вычислить коэффициент вариации (V):
.
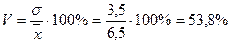Коэффициент вариации свидетельствует о том, что колеблемость стажа работы продавцов весьма значительна и неоднородна.
5.7.4. Определите первый и третий квартили интервального ряда по данным о содержании бракованных товаров в поступившей в магазин партии товара:
| бракованные товары, % (х) | число образцов (f) | накопленная частота S | середина интервала x 
| x f
|
| А | ||||
| до 14 | ||||
| 14-16 | ||||
| 16-18 | ||||
| 18-20 | ||||
| 20 и более | ||||
| Итого | - | - |
Решение:
Первый и третий квартили имеющегося ряда определяем по формулам:
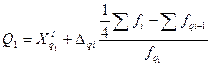= 14+2 
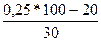= 14,3%;
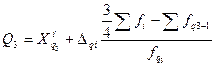= 18+2 
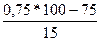=18,0%.
Следовательно, в ряду распределения по данным о бракованных товарах в поступившей партии товара в магазин первый квартиль составляет 14,3%, а третий – 18,0%, т.е. 25% товаров содержат брак, не превышающий 14,3%, а у 75% товаров процент брака не превышает 18%.
5.7.5. Определите 1-й и 9-й децили интервального ряда по данным о содержании влаги в поступившей в магазин партии товара:
| влажность, % (х) | число образцов (f) | накопленная частота S | середина интервала x
| x f
|
| А | ||||
| до 14 | ||||
| 14-16 | ||||
| 16-18 | ||||
| 18-20 | ||||
| 20 и более | ||||
| Итого | - | - |
Решение:
Первый и девятый децили данных таблицы определяем по формулам:
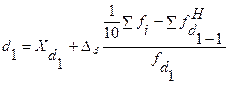= 12+2 
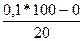= 13%;
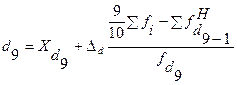= 20+2 
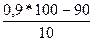=20%.
Таким образом, значения децилей указывают на то, что среди 10% партии товара с минимальным процентом влажности максимальный процент ее составляет 13%, а среди 10% партии товара с наибольшим процентом влажности минимальный процент ее составил 20%, т.е. в 1,54 раза больше.
5.7.6. Имеются данные о времени работы (лет) 24 рабочих в цехе завода:
Стаж рабочих в данном цехе (лет): 4; 3; 6; 4; 4; 2; 3; 5; 4; 4; 5; 2; 3; 4; 4; 5; 2; 3; 6; 5; 4; 2; 4; 3.
Требуется:
1. построить дискретный ряд распределения,
2. дать графическое изображение ряда,
3. вычислить показатели центра распределения, показатели вариации и формы распределения.
Решение:
1. Дискретный ряд распределения стажа рабочих в цехе завода:
| Время работы (лет), (х) | число рабочих, (f) | накопленная частота, (S) |
| итого | - |
2. Представим графическое изображение построенного дискретного вариационного ряда распределения рабочих по времени работы в цехе в виде полигона частот:
|
Полигон частот замыкается, для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном случае х = 1 и х = 7).
3. К показателям центра распределения относятся: средняя арифметическая, мода и медиана.
Средняя арифметическая (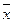)определяется по следующей формуле:
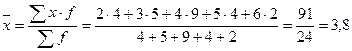лет.
Мода (М0) = 4 годам (4 года встречается 9 раз, т.е. это наибольшая частота f).
Для определения медианы необходимо определить номер интервала, в котором она находится:
NМе =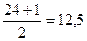 
;
Медиана (Ме) = 4 годам (так как номера 12 и 13 соответствуют 4 годам).
К показателям вариации относятся: размах вариации (R), среднее линейное отклонение (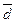
), дисперсия (σ2), среднее квадратическое отклонение (σ), коэффициент вариации (V).
- размах вариации определяем по формуле:
R = Xmax – Xmin = 6 – 2 = 4 года
- для определения среднего линейного отклонения и других показателей вариации построим дополнительную таблицу вычислений:
| количество отработанных лет (х) | число рабочих (f) |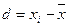 
| 
| 
|
| -1,8 -0,8 +0,2 +1,2 +2,2 | 7,2 4,0 1,8 4,8 4,4 | 12,96 3,20 0,36 5,76 9,68 | ||
| итого | 22,2 | 31,96 |
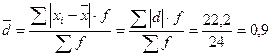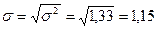лет
лет
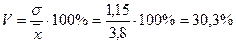
Следовательно, индивидуальные значения отличаются в среднем от средней арифметической на 1,15 года, или на 30,3%.
Среднее квадратическое отклонение превышает среднее линейное отклонение (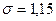
> 
) в соответствии со свойствами мажорантности средних величин.
Значение коэффициента вариации (V = 30,3%) свидетельствует о том, что совокупность достаточно однородна.
Как видно из построенного ранее полигона вариационного ряда распределение рабочих цеха по времени их работы в цехе несимметрично, поэтому определяется показатель асимметрии:
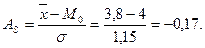
Следовательно, асимметрия левосторонняя, незначительная.
5.7.7. Распределение работников производственного предприятия по размеру месячной заработной платы следующее:
| месячная заработная плата, тыс.руб. | до 15,0 | 15,0-16,0 | 16,0-17,0 | 17,0-18,0 | 18,0-19,0 | 19,0 и более | итого |
| число работников |
Определите коэффициент децильной дифференциации.
Сформулируйте вывод.
Решение:
Коэффициент децильной дифференциации определяется по формуле:
Для этого определяем место децилей:
; 
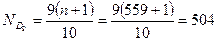
Для расчета численных значений децилей определяем интервалы, в которых они находятся, для чего исчисляем накопленные частоты и результаты записываем в таблицу:
| месячная заработ-ная плата,тыс.руб. | до 15,0 | 15,0-16,0 | 16,0-17,0 | 17,0-18,0 | 18,0-19,0 | 19,0 и более |
| число работников (нарастающим итогом) |
Из таблицы видно, что первая дециль находится в интервале 15,0 - 16,0, девятая дециль находится в интервале 18,0 – 19,0.
Вычислим числовые значения децилей:
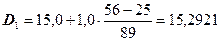тыс.руб. или 15292,1 руб.
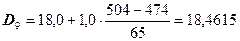тыс.руб. или 18461,5 руб.
= 
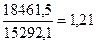
Следовательно, наименьший размер месячной заработной платы 10% наиболее обеспеченных работников в 1,21 раза выше наивысшего размера месячной заработной платы 10% наименее обеспеченных работников.
5.7.8. Имеются следующие данные о возрастном составе работников предприятий потребительской кооперации N - района (лет): 18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29.
Для анализа распределения работников предприятий потребительской кооперации по возрасту требуется:
1. построить интервальный ряд распределения;
2. исчислить показатели центра распределения, показатели вариации и формы распределения;
3. сформулировать выводы.
Решение:
1. Величина интервала группировки определяется по формуле:
года
n (количество интервалов)– мы принимаем равным 7.
Полученный интервальный ряд распределения представим в таблице:
| группы работников по возрасту (лет), х | число рабочих, f | накопленная частота, S |
| 18-21 21-24 24-27 27-30 30-33 33-36 36-39 | ||
| итого | - |
2. Рассчитываем показатели центра распределения (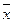, Мо, Ме):
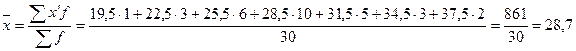года,
где: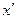 
- среднее значение признака в интервале (центр каждого интервала).
Для определения численного значения моды (Мо) по нашему интервальному ряду определим, что она находится в интервале 27-30 лет, так как наибольшее число работников (f = 10) находится в этом интервале.
Значение моды определяется по формуле:
Мо = х0 + i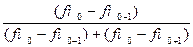 
=
= 
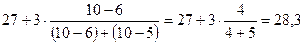года.
Для определения численного значения медианы (Ме) также сначала определяем интервал, в котором она находится:
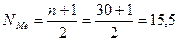
Медианным является также интервал 27-30 лет, так как в этом интервале находятся номера 15 и 16 ряда.
= 
года.
Для расчета показателей вариации составим вспомогательную таблицу:
| группы работников по возрас-ту, лет | центр интервала, (лет),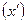 
| f |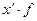 
| 
| 
| 
| 
|
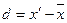
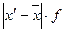
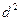
| 18-21 21-24 24-27 27-30 30-33 33-36 36-39 | 19,5 22,5 25,5 28,5 31,5 34,5 37,5 | 19,5 67,5 153,0 285,0 157,5 103,5 75,0 | -9,2 -6,2 -3,2 -0,2 2,8 5,8 8,8 | 9,2 18,6 19,2 20,0 14,0 17,4 17,6 | 84,64 38,44 10,24 0,04 7,84 33,64 77,44 | 84,64 115,32 61,44 0,40 39,20 100,92 154,88 | |
| итого | - | 861,0 | - | 116,0 | - | 556,80 |
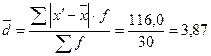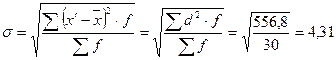года
года
.
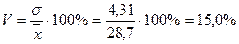Следовательно, вариация возраста у работников предприятий потребительской кооперации не является значительной, что подтверждает достаточную однородность совокупности.
Показатель асимметрии распределения работников по возрасту определяем по формуле:
.
Следовательно, асимметрия правосторонняя, незначительная.
При правосторонней асимметрии между показателями центра распределения существует соотношение:
Мо < Ме <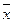
Для данного распределения это соотношение выполняется, т.е.
28,3 < 28,6 < 28,7.
Для имеющегося распределения, учитывая незначительную асимметрию, определяем показатель эксцесса (островершинности):
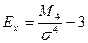, где:
М4 – центральный момент четвертого порядка,
σ4 - среднее квадратическое отклонение в четвертой степени.
= = 
.
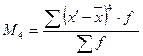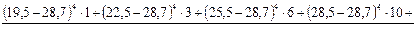
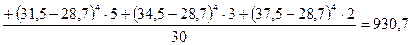
Отрицательное значение эксцесса свидетельствует о плосковершинности данного распределения.
