Управляющий элемент под воздействием регулирующего напряжения изменяет частоту генерации генератора Г. Все управляющие элементы можно подразделить на чисто электронные и электромеханические. Электронные управляющие элементы отличаются безынер-ционностью, малым потреблением мощности от источника регулирующего напряжения, но обычно не позволяет перестраивать гетеродин в широких пределах. Для гетеродинов с отдельными колебательными система-
ми основными видами управляющих элементов являются варикапы (ва-ракторы) и реактивные транзисторы.
Варикап — полупроводниковый диод, работающий при обратном смещении на />п-переходе. Варикапы отличаются небольшими размерами, малой мощностью, потребляемой от цепи управления (ток запертого перехода очень мал), широким диапазоном рабочих частот, высокой механической прочностью и отсутствием микрофонного эффекта.
Емкость варикапа зависит от приложенного напояжения следующим
образом: 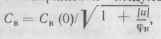 где
где
Св (0) — емкость при и = 0; срк — контактная разность потенциалов (фк =0,8 в для кремния). Графически эта зависимость изображена на рис 9.7. Пределы изменения емкости ограничены пробоем р-п-перехо-
Да ("max) И ВЫХОДОМ НЭ уЧЭСТОК ПрЯ-
мой проводимости («щщ) с увели-чением шунтирующего действия варикапа на перестраиваемый контур гетеродина. Вообще же добротность варикапа зависит от частоты. На низких частотах она определяется в основном активным сопротивлением p-n-перехода (Q„ = соСв/?р_„), а на высоких частотах — объемным сопротивлением полупроводника (QB — 1/шСвл,.). Имеется частота, на которой добротность варикапа максимальна. Значение Qm имеет порядок несколько тысяч на частотах, измеряемых единицами мегагерц, и падает До нескольких десятков на частотах 100 МГц.
При больших амплитудах переменного напряжения в варикапе возникает детекторный эффект, появляется постоянная составляющая тока, которая, создавая падение напряжения на внутреннем сопротивлении источника регулирующего напряжения ыр, управляет варикапом. Чтобы снизить влияние детекторного эффекта, не рекомендуется включать в цепь варикапа омические фильтры с большим сопротивлением. Целесоообразно встречное включение двух варикапов. При этом снижается нелинейность контура, перестраиваемого варикапом. Пример подобной схемы управления частотной настройки контура приведен на рис. 9.8.
В качестве неременных электрически управляемых емкостей иногда используют и обычные диоды при обратном смещении, а также емкости переходов транзисторов.
Управляющими элементами могут быть также реактивные транзисторы или реактивные лампы. Благодаря особой схеме включения в них создается отличный от нуля (или от 180) фазовый сдвиг между током и напряжением. Обобщенная схема реактивного транзистора приведена на
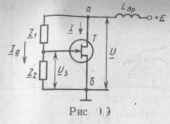
Рис. 9.9
рис. 9.9. В качестве реактивных элементов могут служить активные приборы с большим внутренним сопротивлением. Они поддаются регулировке внешним управляющим напряжением на частотах, где крутизну можно еще считать чисто действительной величиной.
Допустим, что выполняется условие |/д| <С |/|- Тогда проводимость схемы между точками а — б
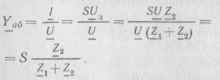
Видно, что проводимость зависит как от сопротивлений Z,, Z2, так и от крутизны активного прибора S. В этом заложена возможность электронного управления проводимостью Уаб, подачей регулирующего напряжения на затвор (базу) реактивного транзистора.
В табл. 9 .1 указаны значения активных сопротивлений и емкостей (или индуктивностей) между точками а б для некоторых простейших видов
сопротивлений Zx и Z*. При этом Уаб== l/Ra6+(l /joiLu6) (или/соС,,,-,). Пре-делы регулировки ограничены запиранием транзистора и чрезмерным током управляющего электрода.
Реактивный транзистор подключается параллельно контуру гетеродина полностью или частично в зависимости от требуемого перекрытия по частоте и допустимого шунтирования контура активным сопротивлением Ra6 (оно уменьшается с ростом крутизны 5).
Электромеханические управляющие устройства отличаются значительной инерционностью, но позволяют по-получить автоподстройку в широком диапазоне частот. Как правило, они имеют в качестве исполнительного механизма электродвигатель с редуктором, перемещающий орган перестройки — ротор переменного конденсатора или вариометра, подстроечный плунжер объемного резонатора или короткозамыкающий мостик резонатора на отрезках линий и т.п.
Электродвигатель является интегрирующим звеном системы АПЧ и в принципе придает ей астатические свойства, т. е. возможность сведения остаточной ошибки регулирования до нуля. Практически этому препятствует неизбежное влияние трения в подшипниках двигателя и в редукторе. Система АПЧ останавливается, когда вращающий момент уравнивается с моментом трения в подшипниках двигателя и в редукторе.
Таблица 9.1
| R | С | R | L | |
| h | С | R | L | R |
| 1+(ыСД)« | /?2 + w2L2 | R*+ co2L- | ||
| S | S (coC/?)2 | SR2 | ||
| La6 | 1 + (шСЯ)2 | SCR | SLR | |
| Sa>*CR ac' | 1 + (шС/?)2 а6 | StfLR ~La* |
Основной областью применения электромеханических управляющих устройств являются широкодиапазонные системы АПЧ малого быстродействия.
В качестве гетеродинов приемных СВЧ-устройств широкое применение находят отражательные клистроны и лампы обратной волны (ЛОВ). Эти генераторные приборы не требуют специальных управляющих элементов, так как частота генерируемых ими колебаний зависит от напряжения на электродах. Для отражательных клистронов наиболее удобным электродом для подачи регулирующего напряжения является отражатель. Это бестоковый электрод, не потребляющий мощности от источника ир и сильно влияющий на частоту генерации.
Типичные колебательные характеристики отражательного клистрона приведены на рис. 9.10. В каждой зоне генерации частота убывает с уменьшением и0тР. Диапазоном электронной перестройки Д/3 считается диапазон частот, в котором мощность генерации не меньше чем 0,5Р,„. Приближенно А/э да l,2/r/Q„, где /г — центральная частота генерации; Q„ — нагруженная добротность резонатора клистрона.
Крутизна 5Г характеристики /г(" отр) в пределах диапазона электронной перестройки обычно имеет порядок долей мегагерц на вольт.
ЛОВ отличаются очень широким перекрытием по частоте при изменении напряжения на замедляющей системе. Для гетеродинных ЛОВ изменение напряжения на замедляющей "з-с от сотен вольт до единиц киловольт вызывает изменение частоты генерации в несколько раз. Подобного перекрытия по частоте не дают другие генераторные приборы. Частота генерации очень мало зависит от характера нагрузки. Типичные зависимости мощности и частоты от напряжения на замедляющей системе изображены на рис. 9. П.. Крутизна характеристики /г(ы:,.с) имеет порядок долей-единиц мегагерц на вольт.
Систему гетеродин — управляк щее устройство принято оиисыват регулировочной характеристике /г ("р)> являющейся зависимость! частоты генерируемых колебаний о регулирующего напряжения в ста™ ческом режиме. При анализе процес сов в системе АПЧ эту характеристи ку обычно линеаризируют и пользу ются ее параметром — крутизной ре гулировочной характеристики:
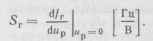
Иногда вместо абсолютной значения частоты берут Д/г - = /г — /г.ном. где/г.и<)%1 —номинальна значение частоты генерации, илт А/г = /г — /э. где /э — эталонно, значение частоты. Типичная регули ровочная характеристика гетеродин; приведена на рис. 9.12. Здесь Д/э — диапазон электронной перестройю частоты. Любые воздействия на /г отличные от воздействия ир, переме щают регулировочную характеристи ку вдоль оси частот, вызывая началь ную расстройку гетеродина Д/г (пунк тир на рис. 9.12). Заметим также, чте в целях нормальной работы системь АПЧ (снижение ошибки настройки] для систем абсолютной частоты и про-

Рис. 9.12
межуточной частоты при /г > /с. необходимо, чтобы знаки 5чд и Sr были противоположны, т. е. 5чд Sr<0. Для систем промежуточной частоты при /,, < /с, наоборот, требуется, чтобы Sh/i Sr >• 0 (знаки одинаковы). Это положение будет проиллюстрировано далее.
Фильтры систем АПЧ в основном аналогичны фильтрам систем АРУ (см. § 8.2). Чаще всего используется однозвенный RC -фильтр нижних частот (см. рис. 8.11, а).
Усилители постоянного напряжения не только усиливают напряжение или мощность регулирующего сигнала, но и переносят его уровень на необходимое значение постоянной составляющей, а также меняют (или не меняют) знак крутизны 5чд. Вообще усиление на постоянном токе можно рассматривать как увеличение абсолютного значения крутизны 5чд в Ку раз. В дальнейшем под 5чд будем понимать крутизну детекторной характеристики с учетом усиления. Чередование элементов фильтр— усилитель в цепи АПЧ безразлично и диктуется конкретными условиями.
§ 9.3. Переходные процессы
в системе АПЧ
и стационарный режим
Математический анализ динамических режимов работы АПЧ с учетом реальных форм детекторной характеристики ЧД и регулировочной характеристики гетеродина имеет серьезные трудности.
В настоящее время изучение поведения реальных систем АПЧ в ди-
намических режимах принято произ водить на моделях, набираемых на аналоговых вычислительных машинах или реализуемых в виде программ для ЦВМ.
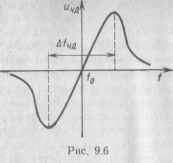
Используя метод информационного параметра, которым в данном случае является частота, систему АПЧ (см. рис. 9.1 или 9.2) можно представить в виде аналоговой модели рис. 9.13. Здесь смеситель (для рис. 9.2) моделируется в виде сумматора, осуществляющего операцию вычитания (или суммирования) частот /п (0 = /г (0 - /с (0- Элемент ФПЧД является функциональным преобразователем, моделирующим детекторную характеристику ЧД вида рис. 9.6. Модель фильтра Ф представляется структурной схемой рис. 8.14, а функциональный преобразователь ФПГ моделирует регулировочную характеристику гетеродина (см. рис. 9.10—9.12); Ку отображает усиление усилителя У. Ясно, что для системы абсолютной частоты (см. рис. 9.1) /п (t) = /г (/.) и надобность в сумматоре, моделирующем смеситель, отпадает.
Для систем не очень высокого быстродействия с инерционностью УПЧ можно не считаться.
Теоретический анализ процессов в системе АПЧ будем проводить для простейшего однозвенного RC-фильтра нижних частот при линеаризованных характеристиках детектирования частотного детектора и регулировочной характеристике гетеродина [171.
Регулирующее напряжение связано с ычд («чд — выходное напряжение цепи частотный детектор — усилитель) дифференциальным уравнением вида
Для системы абсолютной частоты (см. рис. 9.1)
«чд = 5 чд (fr — fr ном) АПЧ =
= 5 чдА/гапч. (9.2)
Для систем промежуточной частоты (см. рис. 9.2, 9.3)
«чд = S4n (/„—/„.„оч)АПЧ г= = 5 чдД/„апч. (9.3)
Здесь индекс АПЧ указывает, что имеются в виду отклонения частоты при замкнутой системе АПЧ.
В свою очередь, если (см. рис. 9.12)
/г~/г.ном — ^гы|) - АД,, (9.4)
то
(/г — /г.ном)аПЧ = Л/ЛПЧ =
= -Sr«p+A/r, (9.5)
(fn — /п.ном)аПЧ = Д/пАПЧ = (/,—/<•,—
—/г-ном + /с.ном)апч = А/гАПЧ—- А/с =
= Sr«n-A/c + A/r, (9.6)
где А/с = /сном — /с — отклонение частоты сигнала от того значения, которое дает / п = /п.„0м при /г= = /г.ном- В (9.6) было положено /,. > > /с и /,, = /г — /с-
Очевидно, при /г < /с (/„ = /с —
— /г) получилось бы А/ГАПЧ = = А/с — А /гАпч и для правильной работы- системы АПЧ пришлось бы изменить знак 5чд- Видно, что правые части уравнений (9.2) и (9.3) отличаются только наличием или отсутствием начальной расстройки частоты сигнала А/к. Подставляя значение «чд (9.3) в уравнение (9.1) с учетом
(9.6), получим RCd££ 4 -(1 4- 5чд5г)х
Х«р = 5Чд (А/г — А/с)= 5Чд А/нач, где А/нач = (Д/г — Д/с) — начальная расстройка. Находя из (9.6)
«р s; (Л^,1ач " " Л/"Апч), ^f- =
D д/,,апч
= — тг т. - и подставляя это
ог at
в уравнение для ыр, получим
RC dA/nAI14 + (1 + S4n Sr) А/папч - ot
= А/„а., (9.7)
Величины Д/г и ЛД. изменяются одновременно случайным образом или детерминированно, обычно независимо одна от другой. Рассмотрим случай, когда величина Д/нач изменяется скачком и после изменения остается постоянной. Тогда уравнение (9.7) можно легко решить в виде
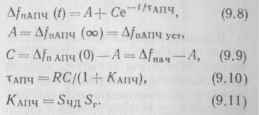
Видно, что здесь, так же как и для системы АРУ, эквивалентная постоянная времени системы тАпч в 1 4-4- /САпч раз меньше постоянной времени /?С-фильтра, что свидетельствует о более быстром протекании процесса установления Д/пАпч (t) в замкнутой цепи АПЧ, чем «р (t) в фильтре с постоянной времени RC.
Величина /Слпч характеризует глубину регулирования системы АПЧ и точность ее работы (остаточную ошибку настройки УПЧ приемника или гетеродина). Действительно, из (9.9), (9.7) установившееся значение ошибки

где А/нач — Д/г —■ А/с — начальная ошибка настройки приемника (его УПЧ для системы промежуточной частоты и гетеродина — для системы абсолютной частоты).
Закон установления расстройки можно найти после подстановки (9.9) в (9.8) с учетом (9.12):
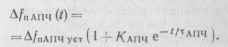
(9.13)
График, отображающий уравнение (9.13), приведен на рис. 9.14.
Время установления ty определим как время, прошедшее от возникновения начальной расстройки (/ = 0) до момента достижения расстройкой значения 1,1 А /пАПЧуст Приравняв (9.13) этому значению, найдем
гу = 2,ЗтАпч (1 + 0,435 In /СА„ч). (9.14)
Ясно, что при использовании системы АПЧ в приемнике ЧМ-сигналов ее быстродействие ограничено требованием отсутствия демодуляции сигнала даже для самой низкой модулирующей частоты. Вместе с тем система АПЧ должна устранять расстройки, происходящие медленно, из-за влияния различных дестабилизирующих факторов, т. е. постоянная времени АПЧ должна удовлетворять условиям

(9.15)
где 7"Дестаб — «период» паразитных изменений частоты.
Эти условия аналогичны таким же условиям для систем АРУ приемников АМ-сигналов. Вообще говоря, система АПЧ неизбежно снижает индекс частотной модуляции сигнала. Это снижение даже на самой низкой частоте модуляции не должно превышать определенного небольшого значения.
Уравнение (У. 12) описывает регулировочную характеристику системы АПЧ в стационарном режиме при условии небольших начальных расстроек, когда справедливы линейные аппроксимации характеристик — детекторной частотного детектора и регулировочной гетеродина. Как видно, регулировочная характеристика есть прямая-, проходящая под углом arctg т -г4 - к оси абсцисс
(рис. 9.15). При больших начальных расстройках начинают проявляться нелинейности элементов системы АПЧ. Аналитический расчет регулировочной характеристики в этом случае очень сложен.
Ограничимся графическим анализом работы системы АПЧ при больших расстройках в стационарном режиме. Для этого объединим в одной системе координат /, ичд, детекторную характеристику ЧД (см. рис. 9.6) и регулировочную характеристику гетеродина (см. рис. 9.12). При этом учтем, что в стационарном режиме иа =
ицд, (см. уравнение(9.1) при Для систем абсолютной частоты,
когда /о = /г -ном. совмещение делается простым изменением направления осей графика рис. 9.12. Для систем промежуточной частоты детекторная характеристика переносится в область частот /г добавлением к каждому значению /„ величины /с.„им
(при /„ •-= /г — /с /Р = /„ + /с). Совмещенные характеристики изображены на рис. 9.16. Если при совмещении они заняли положение / на рис. 9.16, то это означает, что приемник (его УПЧ или гетеродин) настроен точно и вмешательства системы АПЧ не требуется. При этом ычд — 0.
При изменении частоты, генериру" емой гетеродином, из-за влияния дестабилизирующих факторов (вообще по любой причине, кроме действия напряжения ир — ичд) регулировочная характеристика перемещается вдоль оси частот. Точно так же при изменениях частоты сигнала переме-
щается детекторная характеристика ЧД.
Кривая 2 на рис. 9.16 отображает состояние системы при отклонении частоты гетеродина на величину д/г относительно /ГНОм- При этом на выходе ЧД появляется положительное напряжение, которое снижает частоту колебаний, генерируемых гетеродином (см. рис. 9.12). Снижение частоты /г будет происходить до тех пор, пока не уравняются напряжение «чд, создаваемое частотным детектором, и напряжение ир = «чд, необходимое для генерации данной частоты. Очевидно, этому положению соответствует точка пересечения характеристик ЧД и гетеродина. Таким образом, при работе АПЧ вместо начальной ошибки д/г будет ошибка настройки / г — /гном - д/г апч < < д/г. Легко видеть, что эта остаточная ошибка настройки при линейных характеристиках ЧД и гетеродина определяется по формуле (9.12).
Система АПЧ будет при любых обстоятельствах снижать ошибку настройки, если начальные расстройки лежат в пределах «области втягивания» (или «области захвата»), ограниченной точками пересечения с осью частот регулировочных характеристик, являющихся внутренними касательными детекторной характеристики ЧД (рис. 9.17). В пределах этой области имеется единственная точка пересечения детекторной и регулировочной характеристик, в которой выполняется условие правильной работы: S4ASr<0 (при /г>/с).
Если начальная расстройка выходит за пределы «области втягивания», но остается в пределах «области удерживания» (см. рис. 9.17), ограниченной точками пересечения с осью частот регулировочных характеристик, являющихся внешними касательными детекторной характеристики ЧД, то появляются три точки пересечения детекторной и регулировочной характеристик. Условие подстраивающего действия АПЧ выполняется в двух точках — / и 3. При работе в точке / система АПЧ резко снижает

ошибку настройки, а при работе в точке 2 она не является устойчивой, так как при этом любые случайные отклонения частоты /г поддерживаются системой АПЧ и генерируемая частота переходит в точку / или 3. В последнем случае система АПЧ размыкается и оказывается неработоспособной.
Таким образом, при начальной расстройке в пределах области удерживания, но вне пределов области втягивания система АПЧ может сохранять или не сохранять работоспособность. Это зависит от того, как начальная расстройка попала в эту область. Если происходило медленное увеличение расстройки без перерыва в приеме сигнала, то система АПЧ будет правильно работать до тех пор, пока начальная расстройка не выйдет за пределы области удерживания. Наоборот, если происходило уменьшение начальной расстройки, то система АПЧ не начнет правильно работать до тех пор, пока начальная расстройка не войдет в пределы области втягивания.
Описанные процессы соответствуют регулировочной характеристике системы АПЧ, примерный вид кото-

телыю, из рассмотрения треугольников abc и bed на рис. 9.17 следует, что
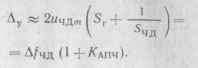
Рис. 9.18
рой изображен на рис. 9.18. Характерным является наличие «гистерезис-ных петель», обусловленных различием областей втягивания и удерживания. На рис. 9.18 условно показаны скачкообразные переходы с характеристики при наличии АПЧ на характеристику без АПЧ и наоборот. Фактически этот переход происходит по некоторым сложным траекториям, примерный вид которых показан на рис. 9.18 пунктиром. Различие областей втягивания и удерживания обусловлено специфической формой скатов детекторной характеристики ЧД. Чем выше линейность скатов этой характеристики, тем меньше отличие областей втягивания и удерживания, Ширина области удерживания (а следовательно, и области втягивания) пропорциональна полосе пропускания частотного детектора и тем больше, чем больше / Сапч • Действи-

(9.16)
Рассмотрим еще одно явление, которое может иметь место в системах промежуточной частоты. Пусть произошло изменение частоты гетеродина или частоты сигнала настолько большое, что промежуточная частота стала образовываться способом /п= /о — /г вместо принятого в данной системе способа /п = /г — /с. Тогда при совмещении детекторной и регулировочной характеристик (см. рис. 9.16) вместо того, чтобы прибавлять к каждому значению /п величину /с-ном. необходимо будет из /,.„„„ вычесть текущее значение /„ (/г= =/с-ном — /п)- При этом детекторная характеристика перевернется, а знак Smx на ее рабочем участке изменится на обратный. Таким образом, изменение способа образования промежуточной частоты в системе АПЧ промежуточной частоты эквивалентно обращению детекторной характеристики ЧД. Иллюстрацией этого является рис. 9.19. Видно, что система АПЧ, рассчитанная на работу при частоте /п /г — /с. начинает не настраивать гетеродин (приемник), а, наоборот, расстраивать его при /„ = /с — ■— /,., так как устойчивыми точками являются точки /' и 3'. Точка 2' вблизи номинального значения частоты гетеродина/' г.ном является неустойчивой. Любые случайные отклонения от нее поддерживаются системой АПЧ. Подобная работа системы АПЧ называется ложной.
Во избежание ложной работы системы АПЧ необходимо принимать меры для того, чтобы перескоки частоты гетеродила или сигнала не превышали
2 /п- ном •
При изменении способа образования частоты /„ необходимо переключать полярность выходного напряжения частотного детектора, т. е. нзме-
Я2
нять знак крутизны его детекторной характеристики.
Вообще же надежной работа системы АПЧ является только в пределах области втягивания (захвата). При выходе начальной расстройки за ее пределы в большинстве случаев требуется вмешательство оператора (ручная подстройка гетеродина в пределы области втягивания) или переход системы АПЧ в режим автоматического поиска по частоте.
§ 9.4. Устойчивость систем АПЧ
Система АПЧ, являясь замкнутой системой обратной связи, способна к самовозбуждению. Неустойчивость системы АПЧ проявляется в виде паразитной частотной модуляции сигнала, а если эта паразитная ЧМ достаточно глубока, — то и в виде амплитудной модуляции, связанной с неравномерностью частотных характеристик приемника.
Процесс самовозбуждения начинается со случайного изменения частоты (гетеродина, сигнала или промежуточной), вызывающего появление напряжения на выходе ЧД. Если это напряжение, превращаясь в регулирующее напряжение, поддерживает первоначальное отклонение частоты, то система АПЧ является неустойчивой.
Поскольку инерционность системы АПЧ в приемных устройствах АМ-сигналов может быть весьма малой (в этом случае она не ограничена условием отсутствия демодуляции ЧМ-сигнала), при анализе устойчивости приходится учитывать дополнительные фазовые сдвиги в элементах петли АПЧ — УПЧ, ЧД, усилителях. В первом приближении фазовые характеристики этих элементов можно считать линейными и тогда вызываемый ими дополнительный фазовый сдвиг Ф=—Йтп, где т3—время запаздывания сигнала при прохождении через указанные элементы.
Для общности будем рассматривать систему промежуточной частоты (с УПЧ) и использовать критерий ус-^ тойчивости Найквиста. Разомкнем си-
I7
стему в точке ввода регулирующего напряжения (рис. 9.20) и будем считать, что случайное отклонение промежуточной частоты от /п.„оМ произошло за счет возмущающего воздействия на входе uv. Выделим из спектра возмущения одну частотную составляющую с амплитудой U qbx и
проследим ее преобразования в петле АПЧ.
Наличие напряжения с комплексной амплитудой U qbx на входе ир
вызовет отклонение частоты гетеродина с комплексной амплитудой
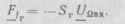 (9.17)
(9.17)
Если /п == /г —/с, то отклонение промежуточной частоты
 (9.18)
(9.18)
С учетом запаздывания в элементах петли АПЧ амплитуда напряжения на входе фильтра
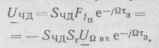 (9.19)
(9.19)
Регулирующее напряжение с учетом действия фильтра системы АПЧ (ФНЧ) имеет амплитуду
 (9.20)
(9.20)
Петлевое усиление цепи АПЧ

Пусть фильтр цепи АПЧ — одно-звенный /?С-фильтр нижних частот, для которого Ф (уй) = 1/(1 4- jQRC). Тогда
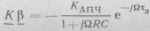
(9.22)






