из (2.2) можно получить выражение
п
Здесь,И (0 = %gt(t) exp (t)\
комплексная гауссова случайная величина, перемножаемая с полезным сигналом и образующая мультипликативную помеху.
Модуль \М (/)| представляет собой рэлеевскую случайную величину с плотностью вероятности
(2.4)
т. е. имеются амплитудные замирания принятого сигнала по рэлеевско-му закону со средней величиной т { \М\ } Vn :2 ом и дисперсией «•||А1|«} 2а%,
Фаза величины М распределена равномерно на интервале [—л, л] и учитывает фазовый множитель ехр|/(ф„— со0т)1 из (2.2).
Формулу (2.3) используют для описания входного колебания приемника, когда зондирующий сигнал отражается от медленно флуктуирующих целей малых размеров. Следствием последнего является то, что искажением комплексной огибающей сигнала Е (/) при отражении от цели можно пренебречь. Принятый сигнал (2.3) отлич'ается от зондирующего сигнала (2.1) четырьмя параметрами: случайными амплитудой |М(/)| и фазой arg (/И (/)), доплеровским смещением частоты Q;i и запаздыванием сигнала т. Амплитуда и фаза определяются отражающими свойствами цели, изменением условий распространения радиоволн и являются случайными величинами. Доплеровское смещение частоты и запаздывание сигнала определяются скоростью и дальностью до цели соответственно и являются неизвестными неслучайными величинами.
Если в системах радиосвязи за
интервал передачи информации Т изменяются характеристики канала распространения радиоволн (например, состояние тропосферы в зависимости от метеорологических условий), то считается, что мультипликативная помеха М (/) является быстрой, так как время ее корреляции т„< Т. В радиолокации такое же явление наблюдается при большой скорости изменения отражательных характеристик цели (например, за счет случайных «рысканий» летательного аппарата по направлению и его вибраций).
Указанные явления вызывают расширение спектра принятого сигнала по сравнению с излученным. Подобные каналы называют каналами с доплеровским (частотным) рассеянием, приводящими к время-селективным замираниям огибающей сигнала в процессе передачи (извлечения) информации.
Для радиолокационного зондирующего сигнала (2.1) отраженный от цели сигнал на входе приемника можно представить в виде
«c(0 = Re{S(/)exp(/a>e*)}t (2,5)
где S (t) Е (/ — т) Мд (/ — т/2) — комплексная огибающая сигнала, состоящая из произведения двух комплексных огибающих: Е (t) — зондирующего сигнала и Мд (/) — мультипликативной помехи, вызванной в основном доплеровскими флуктуация-ми отраженного сигнала.
Член т/2 в множителе /Ид (t — — т/2) обусловлен тем, что сигнал, приходящий на вход приемника в момент времени t, излучается передатчиком в момент времени /— т и отражается от цели в момент времени t — т/2.
Рассмотрим отличие записи сигнала (2.5) при быстрой мультипликативной помехе от сигнала (2.3) при медленной помехе.
В (2.5) отсутствует доплеровское смещение частоты йд, а имеется случайный процесс /Ид (/), энергетический спектр бд (/) которого связан с
доплеровским рассеянием. Среднее доплеровское смещение частоты
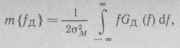(2.6) а дисперсия
Приведем еще одну наиболее простую модель принятого сигнала, часто используемую в радиосвязи в пределах прямой видимости. На небольшом пути распространения характеристики канала иногда можно считать неизменными во времени, т. е. М (/) = = М, а доплеровское смещение йд и задержку т — постоянными/При этих условиях сигнал на входе приемника записывается в виде
ие (t) = Re {ME (t — т) exp |/ (co0 +
+ Йд)^-/со0т + /Фо]}. ' (2.8)
Таким образом, рассмотрены три модели принимаемого сигнала, прошедшего однолучевой канал. Если зондирующий (передаваемый) сигнал (2 .1) является детерминированным, то сигналы на входе приемника из-за прохождения через канал становятся случайными процессами с флуктуирующими огибающей и фазой.
§ 2.2. Сигналы на входе приемника, отраженные пространственно-распределенными рассеивателя ми
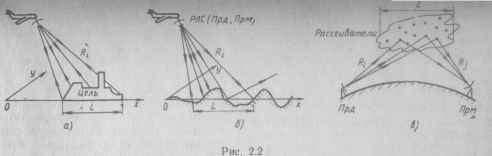
При радиолокации протяженных по дальности (L) целей (рис. 2.2, а), отражении радиоволн от протяженных (L) неровных поверхностей (земной, водной, рис. 2.2, б), а также в радиосистемах передачи информации, использующих ионосферные и тропосферные каналы (рис. 2.2, в), радиоволны от места передачи (Прд) в пункт приема (Прм) распространяются по большому числу лучей (путей). При этом времена запаздывания
принимаемых сигналов (относительно переданного) по отдельным <-м лучам различны: тг 2/?г/с — в радиолокации (рис. 2.2, а, б), тг =| = (Ri — Rj)lc — при передаче информации (рис. 2.2, в), где Rt, Rj~ соответствующие расстояния до элементарных рассеивателей цели, поверхности или тропосферных (ионо-i сферных) образований; с — скорость распространения радиоволн. Кроме того, могут быть и радиальные скорости vt = dRi/dt относительно каждого отражателя (рассеивателя), образующие доплеровские сдвиги частоты Йд,- = со02иг/с.
Таким образом, рассматриваемые каналы имеют рассеяние по двум параметрам: времени запаздывания т и доплеровской частоте Од.
Если излучаемый сигнал представить в виде (2 .1), то принимаемый от любого 1 -го отражателя (рассеивателя) сигнал с точностью до постоянного множителя может быть описан выражением
где gi (t, т() — комплексный случайный гауссов процесс, независимыми переменными которого являются время и задержка (пространство); зависимость от / является следствием изменения во времени ориентации и композиции отражателей (рассеивателей), участвующих в формировании г'-го отраженного сигнала; фг (t) — случайная фаза, которая считается равномерно распределенной на интервале [—л, л].
Сделаем допущение, что отраженные сигналы с различных дальностей Ri статистически независимы. Тогда результирующий сигнал на входе приемника будет являться суперпозицией 1 -х отраженных сигналов:
где gi (/) и ф; (t) — случайные и взаимонезависимые величины при i = k
и i Ф k, i, k = 1, N.
Комплексная огибающая результирующего сигнала
(2.11)
т. е. происходит «размывание» (искажение) закона модуляции Е (/) зондирующего сигнала, что является следствием отражения радиоволн от пространственно-распределенных рас-сеивателей. Типичный случай иллюстрируется рис. 2.3, когда зондирующий импульс имеет длительность ти (рис. 2.3, а), а сигнал на входе приемника, отраженный от пространственно-распределенных рассеивателей вида рис. 2.2, расширяется во времени до величины Lie -f ти (рис. 2.3, б). Видно, что огибающая S (t) принятого сигнала состоит из задержанных (запаздывающих) копий огибающей Е (/) зондирующего сигнала, которые взвешиваются с комплексными гауссовыми величинами g (t, т) и суммируются (интегрируются).
Цель, или рассеиватели, протяженные по дальности, вызывают частотно-селективные замирания принятого сигна-л а. Представим преобразования
Фурье огибающих переданного и принятого сигналов в виде
(2.12)
Если предположить, например, что передается сигнал, преобразование Фурье огибающей которого
где АД, — ширина спектра сигнала (рис. 2.4, а), то при условии Д/с 2> > ci'L преобразование Фурье принятого сигнала 5 {/} будет соответствовать рис. 2.4, б. Амплитуды составляющих на частотах, отстоящих более чем на cIL [Гц], можно считать статистически независимыми, поэтому такое поведение спектра называют частотно-селективными замираниями. Если же ширина спектра сигнала Д /с -С c/L, то огибающая принятого сигнала будет неискаженной, что соответствует моделям принятого сигнала, рассмотренным в §2 .1.
Плотность вероятности для огибающей сигнала на входе приемника, отраженного от пространственно распределенных рассеивателей обычно является рэлеевской (2.4), иногда райсовской или логарифмически нормальной.
