Полоса пропускания таких филы ров обратно пропорциональна обще му времени задержки и выражаете? примерным равенством П да (1 -т -г-2)/тлг. Для получения узкой полось пропускания физическая длина линш задержки должна быть большой, чт< является недостатком этих фильтров
Известно большое количество спо собов получения заданной АЧ> фильтра на ПАВ. В общем случае ре зультирующая АЧХ фильтра зависи-сложным образом от законов аподи зации входного и выходного ВШП Однако на практике для упрощенш расчета и реализации фильтра выход

Рис. 4.24
ной ВШП делают неаподизованным. Можно показать, что при этом АЧХ фильтра определяется соотношением

АЧХ выходного ВШП |#вых вшп (/(о) | обычно выбирают в несколько раз шире, так что АЧХ всего фильтра практически определяется только входным ВШП, т. е. \Н (/со)| да «\Н_ъх вшп (/<">)|.
При выборе аподизации входного ВШП полезно знать, что ВШП с эквидистантным (на равном расстоянии) расположением электродов имеет симметричные АЧХ; кроме того, если закон аподизации симметричен относительно центрального электрода, то ФЧХ фильтра линейна. Помимо аподизации входного ВШП для получения нужной формы АЧХ используют изменение ширины электродов, удаление части электродов, неэквидистантную расстановку электродов, включение дополнительных электродов на пути распространения ПАВ от входного к выходному ВШП.
Заметим, что прямоугольная АЧХ фильтра нереализуема, так как его импульсная характеристика (sinr)/r должна иметь бесконечную протяженность. Практически размеры пьезо-подложки ограничены, следовательно, ограничено число отводов от линии задержки, а значит, и длительность импульсной характеристики, что, в свою очередь, приводит к искажениям АЧХ. Для уменьшения этих искажений функцию smtlt умножают на сглаживающую функцию, в качестве которой используют функции Хэм-минга, Кайзера, Дольфа—Чебышева и др.
Часто применяемая функция Хэм-минга имеет вид g (хп) = 0,54 -f-+ 0,46 cos [2л (хп — 0,5L)/L], где хп — координата п-то электрода; L — длина ВШП.
Для улучшения прямоугольности АЧХ при заданном уровне неравномерности в полосе пропускания проводят оптимизацию АЧХ с помощью ЭВМ. При этом в качестве первого приближения берут либо функцию smtlt, либо ее произведение на одну из сглаживающих функций. ЭВМ позволяет успешно проектировать фильтры с несимметричными характеристиками, например фильтры для УПЧ телевизионных приемников (рис. 4.24).
В узкополосных УПЧ ФСИ на ПАВ выполняют обычно в виде резонаторов, связанных друг с другом электрической (как на рис. 4.25), акустической или той и другой связью вместе. Каждый из резонаторов состоит из двух ВШП и двух отражательных решеток, нанесенных на поверхность пьезоподолжки (обычно из кварца, который подвержен меньшему старению и температурным уходам) в виде параллельных канавок или металлических полосок. Такой резонатор является по существу акустическим аналогом оптического резонатора Фабри— Перо, представляющего собой два отражающих зеркала, расположенных параллельно друг другу на расстоянии /лА/2, где m > 1. В результате многократных отражений от зеркала в резонаторе Фабри—Перо устанавли-
вается режим стоячих волн и накапливается большая энергия.
Добротность такого резонатора Q0 = mK /(l — R), где R — коэффициент отражения, достигает значений Qn = 104- 10». в резонаторе на ПАВ отражателями являются периодические решетки с периодом К/2, которые и ограничивают резонансную полость. Коэффициент отражения Г от каждой канавки глубиной л должен быть весьма малым:: Г «0,3 {hiк), причем h/K = 0,014-0,2, так как при большом коэффициенте отражения значительная часть энергии ПАВ переходит в энергию ОАВ и добротность резонатора резко падает. Собственные частоты резонатора /от = /пупав /(2 X X Ьяф), где ЬЭф — эффективное расстояние между центрами отражающих решеток. Максимальная добротность резонатора на ПАВ приближенно оценивается соотношением Q0 max да да Ю4//п, где частота /п измеряется в ГГц. Резонаторы на ПАВ используют в диапазоне частот 0,1—2 ГГц (применение структуры нитрида алюминия на сапфире позволяет повысить частотный диапазон до 3— 4 ГГц, так как скорость ПАВ в этой структуре примерно в 2 раза больше скорости ПАВ в кварце). Вносимые потери в полосе пропускания фильтров составляют 15—3 дБ. При дополнительном снижении потерь до 1—2 дБ эти фильтры можно использовать во входных цепях приемника, что существенно повысит реальную избирательность приемника.
Для того чтобы характеристики фильтра на ПАВ не искажались, он должен быть согласован с источником сигнала и нагрузкой. Эквивалентная электрическая схема ВШП представляется последовательной цепочкой, состоящей из межэлектродной емкости С„, активной R„ и реактивной Х„ составляющих сопротивления излучения. Сопротивление излучения R„ зависит от длины / электрода ВШП и его обычно выбирают равным стандартному сопротивлению 50 Ом, при этом ПК = 108 (ниобат лития) и ПК = = 53 (кварц). Реактивная составляю-

Рис. 4.26
щая Х„ и емкость С0 компенсирую при настройке внешними реактивнь цепями (рис. 4.26). Для широкопол ных фильтров могут потребовав цепи согласования, содержаи несколько индуктивностей, что удобно для микроэлектронного полнения. Поэтому для сопряжеь ПАВ с гибридными ИМС фильтры ПАВ оформляют в виде частотно-бирательных усилительных мик сборок. Для компенсации емкости либо используют микроминиать ные индуктивности, совместимые к структивно с гибридными ИМС, Л1 включают фильтр на ПАВ между д мя усилительными каскадами, hmi щими индуктивную составляют входного и выходного сопротивлен которые и компенсируют емкости входного и выходного ВШП.
§ 4.4. УПЧ с дискретными и цифровыми фильтрами
УПЧ с дискретными и цифровь фильтрами реализуются в виде И. или микросборок. Рассмотрим вна ле УПЧ с дискретными фильтра! В них происходит обработка некв тованных по уровню дискретных i борок из входного аналогового с нала. Алгоритм работы дискретн фильтра также удобно пояснить примере трансверсального филь' (см. рис. 4.22) с тем лишь изменени что обработке подвергаются выбор входного сигнала, взятые в момег времени 1 =пТ. Поэтому все рассуж ния, приведенные ранее относител! принципа формирования АЧХ, дут справедливы и для данного случ
Можно показать, что частотная рактеристика дискретного фильч имеет вид
где Н (/to) — частотная характеристика того же фильтра без дискретизации входного сигнала.
Последнее выражение показывает, что частотная характеристика дискретного фильтра периодически повторяется с периодом 2л/7\ Для реализации однозначной характеристики дискретный фильтр соединяют последовательно с аналоговым фильтром, который выделяет нужную «гармонику АЧХ» дискретного фильтра. При этом требования к крутизне скатов АЧХ аналогового фильтра обычно невысоки.
Рассмотренный фильтр носит название нерекурсивного. Можно получить новые свойства, введя в фильтр обратные связи (рис. 4.27). Подобные фильтры называют рекурсивными. Их частотные характеристики выражаются соотношением

В дискретных фильтрах отсутствуют аналого-цифровой преобразователь (АЦП) и цифроаналоговый преобразователь (ЦАП), что упрощает фильтр аппаратурно и позволяет фильтровать более широкополосные сигналы при недостаточном быстродействии АЦП и ЦАП. В этом состоит преимущество дискретных фильтров перед цифровыми. Хорошие возможности для построения дискретных фильтров дают приборы с зарядовой связью (ПЗС),
отличающиеся сравнительно высоким быстродействием и низким потреблением мощности.
Фильтры на ПЗС являются транс-версальными фильтрами, принцип действия которых уже пояснялся (см. рис. 4.22). Линии задержки (ЛЗ) представляют собой последовательный набор МОП-конденсаторов, в которых информация сохранится в виде зарядовых пакетов. Динамический диапазон ЛЗ на ПЗС достигает 40 дБ.
Пример ФСИ для УПЧ связного приемника на ПЗС: нерекурсивный фильтр с 600 весовыми коэффициентами выполнен на одном кристалле площадью 16 мм2, затухание в полосе задерживания 76 дБ, полоса пропускания 2,2 кГц, центральная частота 25 кГц, тактовая частота 100 кГц.
Фильтры на ПЗС могут перестраиваться — так называемые программируемые фильтры и фильтры с коммутируемым взвешиванием.
В программируемом фильтре выборочные значения сигнала с отводом ЛЗ на ПЗС подаются на затворы МОП-транзисторов, на стоки которых поступают напряжения, пропорциональные весовым коэффициентам. Эти напряжения формируются программным способом и хранятся в цифровом ЗУ. Взвешенные значения сигнала снимаются с истоков МОП-транзисторов и подаются на сумматор.
Программируемые фильтры, весовые коэффициенты которых принимают лишь два значения (0 или 1), получили название фильтров с коммутируемым взвешиванием (рис. 4.28). В таком фильтре входной сигнал по-
следовательно считывается с отвода каждого элемента задержки 7' на ПЗС, перемножается на соответствующий весовой коэффициент (0 или 1) и взвешенные значения сигнала суммируются, формируя выходной сигнал. Весовые коэффициенты 0 или 1 легко изменяются программным способом.
Перечислим преимущества фильтров на ПЗС перед фильтрами на ПАВ:
полностью интегральное исполнение;
возможность работы на частотах менее 10 МГц (фильтры на ПАВ имеют большие габариты);
обработка сигналов длительностью до 100 мс, в то время как ЛЗ на ПАВ при приемлемых габаритах дают задержку около 10 мкс;
возможность перестройки за счет изменения тактовой частоты.
Добавим также, что в радиоприемниках фильтры на ПЗС используют для согласованной фильтрации, корреляционной обработки и т. д.
Применение цифровых фильтров в УПЧ связано прежде всего с возможностями реализации в них достаточно сложных, но высокостабильных АЧХ и ФЧХ. Например, в приемниках некоторых радиолокационных станций УПЧ может содержать «гребенку» узкополосных фильтров порядка нескольких сотен и даже тысяч при сравнительно низкой промежуточной частоте. Очевидно, цифровая реализация в данном случае является наиболее предпочтительной. Другой пример — многоканальный приемник с повышенными требованиями к идентичности АЧХ и ФЧХ отдельных каналов в реальных условиях работы. Поскольку идентичность характеристик каналов в наибольшей степени определяется идентичностью характеристик в УПЧ, реализация их в цифровом виде практически устраняет основную причину неидентичности.
Наконец, следует подчеркнуть, что использование в УПЧ цифровых согласованных фильтров при оптимальной обработке сигнала в приемнике позволяет получить выигрыш.
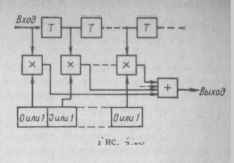
Рис. 4.28
близкий к расчетному в реальных у ловиях работы, тогда как в аналог! вых фильтрах этот выигрыш при изм нении температуры, старении согл сованного фильтра и других дестаб лизирующих факторах может быть с щественно меньше расчетного.
Переходя к схемотехнике цифр вых фильтров, отметим, что их час строят по алгоритму нерекурси ных и рекурсивных дискретных филь ров, однако в отличие от последм здесь обрабатываются двоичные код вые последовательности сигнала, а дискретные выборки из него.
Цифровой фильтр (ЦФ) работа следующим образом (рис. 4.2£ В АЦП в моменты времени I *= п (Т — период дискретизации) значен: входного сигнала UB% (пТ) преобр зуются в двоичную кодовую пос.г довательность, которая поступает арифметическое устройство (АУ). А содержит сумматоры, элементы нам ти в виде набора двоичных элементе число которых равно числу разряд R, и перемножители. Перемножите, реализуют весовые коэффициенты с аи а2, aN и &1( Ьг, ■ Ьм " г разрядно перемножают все разря, входного числа на каждый из разр дов числа, представляющего весов коэффициент, затем эти произведен суммируются. Число двоичных разр дов для представления весовых > эффициентов R„tb изменяется от 4 6 (аппаратурная реализация ЦФ)
16 и более (реализация ЦФ на ЭВМ). Для сохранения информации о сигнале число разрядов произведения должно равняться R + R0tb, однако для упрощения аппаратурной реализации это число сокращают за счет младших разрядов, при этом получается шум округления с дисперсией Д2,ь/12, где Д0>ь—перепад уровней, соответствующей отбрасываемому разряду произведения.
При синтезе линейных ЦФ используют три основных алгоритма: линейные разностные уравнения, временную свертку и дискретное преобразование Фурье (ДПФ).
В соответствии с линейным разностным уравнением

выходную последовательность находят по схеме ЦФ, представленной на рис. 4.27. Такой ЦФ называют рекурсивным, так как выходной сигнал у (kT) в некоторый момент времени kT зависит от входного сигнала х (кТ — пгТ) и выходного сигнала в предшествующие моменты времени.
Цифровые фильтры, описываемые уравнением временной свертки
N
y(kT) = 2* (kT—mT) h (mT), так-
т = 0
же подчиняются предыдущему уравнению, если в нем положить ат = = h (mT), bm = 0, и называются нерекурсивными (они не зависят от выходного сигнала).
При реализации ЦФ по алгоритму ДПФ сначала вычисляют ДПФ для входного сигнала. Далее дискретные значения спектральных составляющих х (kQ) умножают на требуемые значения заданной АЧХ Н (kQ) и вычисляют обратное ДПФ от полученного произведения. При этом для уменьшения количества вычислительных операций часто применяют алгоритм быстрого преобразования Фурье.
При анализе и расчете часто ис-
пользуют передаточную функцию ЦФ которая представляет собой отношение г-преобразования входного и выходного сигналов фильтра и может быть записана в виде:
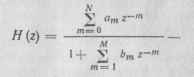
— для рекурсивного фильтра;

—для нерекурсивного фильтра,
где ат, Ьт — коэффициенты разностного уравнения.
При другой форме записи для рекурсивного фильтра имеем

где гг1 и zpi — нули и полюсы функции Н (г) на плоскости г.
Передаточная функция нерекурсивного ЦФ не имеет полюсов, поэтому он абсолютно устойчив. Рекурсивный ЦФ устойчив, если полюсы расположены внутри единичного круга плоскости z.
Прямую форму реализации рекурсивного ЦФ обычно используют для фильтров не выше второго порядка, что связано с накоплением ошибок. Наиболее часто применяют последовательную (каскадную) или параллельную структурную схему ЦФ. При последовательной схеме функция И (z) записывается в виде произведения передаточных функций звеньев первого и второго порядков:
Реализация, например, сомножителя второго порядка соответствует структурной схеме рис. 4.30. При представлении функции Н (г) в виде суммы передаточных функций звеньев первого и второго порядков:

удобна параллельная реализация ЦФ (рис. 4.31). Реализация звена второго порядка показана на рис. 4.32.
Нерекурсивные ЦФ обычно имеют прямую форму реализации. В этом случае, как указывалось, весовые коэффициенты равны дискретным значениям импульсной характеристики. Нерекурсивные ЦФ можно выполнить и по каскадной схеме. При этом передаточная функция нерекурсивного ЦФ представляется в виде произведения передаточных функций звеньев первого и второго порядков:

Здесь коэффициенты Аи и А1} определяются через нули передаточной функции.
Пример реализации звена второго порядка нерекурсивного фильтра показан на рис. 4.33. Так как основу каскадной схемы ЦФ составляет звено второго порядка, рассмотрим его реализацию более подробно. Пусть необходимо реализовать резонансный ЦФ, передаточная характеристика которого имеет вид Н (г) — (1 — — az~l)l(\ — bz~l -f cz-2).
Реализация по прямой форме соответствует рис. 4.34. Рассмотрим частный случай сод = 2л/Т — 4w0. Тогда Н (г) =1/(1 + cz~2) и реализация существенно упрощается



Дь
Рис. 4.36
(рис. 4.35). АЧХ фильтра (при подстановке z~x = е-"°т) имеет вид
\Н (/со)| - \IV\ + 2с cos 2wT + с2 и представлена на рис. 4.36.
Для получения добротности Q = 100 и Q — 1000 задание коэффициента с с точностью до Ас — Ю-2, Ас = Ю-3 приводит к изменению добротности AQ/Q = 0,1, AQ/Q = 0,01.
Таким образом, для представления с с требуемой точностью необходимо иметь не менее 10 двоичных разрядов.
Рассмотренный резонансный ЦФ может быть выполнен по последовательной схеме согласно рис. 4.37.
АУ данного фильтра состоит из двух БИС: многоразрядного сумматора и умножителя последовательного действия. Регистры /— 4, входящие в АУ, имеют следующие назначения: регистр / является выходным регистром, регистр 2 необходим для записи частных произведений умножителя, регистр 3 сдвигает кодовую последовательность на два такта, в регистр 4 записывается коэффициент с.
Одно выходное значение функции у (kT) вычисляется за время, оцениваемое величиной Тб да Л/рМр/2, где ^р> Мр — разрядность множителя и множимого; tz — быстродействие одноразрядного сумматора. Минимальный период дискретизации сигнала Т > Тб, следовательно, максимальная рабочая частота рассмотренного фильтра
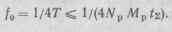
Рабочая частота фильтра может быть увеличена введением параллельной обработки разрядов чисел несколькими АУ, при этом частота /„ да да \/(Mpts) повышается, но и объем аппаратуры также возрастает.
ГЛАВА 5
ПРЕОБРАЗОВАТЕЛИ ЧАСТОТЫ
§ 5.1. Общая теория преобразования частоты
В преобразователе частоты происходит изменение несущей частоты колебания сигнала.
В гетеродинном преобразователе частоты сигнал и колебания местного генератора (гетеродина) одновременно воздействуют на нелинейный элемент (или на элемент с переменным параметром), в результате чего возникает колебание, имеющее в своем составе составляющие с частотами сигнала fe и его гармоник, гетеродина /г и его гармоник и большое число комбинационных составляющих с частотами /„ - \nfr ± mjc\, где пит — целые числа. Одну из этих комбинационных частот, используемую в качестве новой несущей частоты выходного сигнала, называют промежуточной частотой /,,.
С точки зрения минимизации искажений информации при преобразовании частоты и улучшения избирательности при наличии мешающих сигналов преобразователь частоты для сигнала должен быть линейным, т. е. в нем не должны порождаться гармоники частоты сигнала. Это условие выполняется более или менее точно, если сигнал £/,. является «малым». При этом размах сигнала захватывает лишь небольшой участок характеристики преобразовательного элемента и ее можно считать линейной на этом участке.
По отношению к колебаниям гетеродина нелинейность (параметрич-ность) преобразовательного элемента должна проявлять себя возможно сильнее. Обычно это требует значительных амплитуд гетеродинного напряжения U,.. Таким образом, в -подавляющем большинстве случаев выполняется условие Uv << U г. До тех пор, пока выполняется это неравенство, свойства преобразователя частоты не зависят от амплитуды
сигнала и всецело определяются свс ствами преобразовательного элемент амплитудой гетеродинного напр жения и стабильностью его коде(ний.
В этих условиях любая из ком(национных составляющих несет же информацию, что и первичный а нал, и может быть принята за коле(ние промежуточной частоты. Состг ляющая промежуточной частоты вы; ляется фильтром, включаемым в t честве нагрузки преобразовательно элемента в цепь его выходного эле трода.
Со спектральной точки зренк как видно из изложенного, проио дит перенос спектра сигнала в облас промежуточной частоты без наруц ния амплитудных и фазовых акт шений его составляющих.
Роль нелинейных или параметр ческих элементов в современных пр образователях частоты обычно выпс няют транзисторы — биполярные полевые, а также диоды — вакуу ные и полупроводниковые. В ь честве фильтров промежуточной ч; тоты используют одиночные коле(тельные контуры, двухконтурн фильтры и фильтры сосредоточенн избирательности.
Отметим, что преобразовательш элемент может иметь в качестве пр образующего параметра активш параметр (активное сопротивлен1 или реактивный параметр (емкое либо индуктивность). Чаще испо/ зуются преобразователи частоты с £ тивными преобразующими параметр ми, так как они одинаково эффект» но работают и при понижении (иг более распространенный случай) при повышении частоты. Преобр зователи частоты с реактивны преобразующими элементами эффе тивно работают только при повьш нии частоты и считаются разновидг стями параметрических усилителе
Преобразовательные элементы, обладающие усилительными свойствами, можно использовать для генерации гетеродинирующих колебаний. В иных случаях требуются отдельные гетеродины. Часто в литературе преобразовательные элементы подобного вида называют смесительными (в них происходит смешение колебаний сигнала и гетеродина). В общем случае преобразователь частоты включает в себя преобразующий элемент (смеситель), гетеродин и фильтр, выделяющий колебание промежуточной частоты.
В основу классификации преобразователей частоты обычно кладут тип преобразовательного элемента и особенности схемотехники. Так, различают транзисторные, диодные, перемножительные преобразователи частоты. В последних в основе преобразования частоты лежит математическая операция перемножения колебаний сигнала и гетеродина и соответственно любые схемы перемножения, работоспособные на достаточно высоких частотах, могут применяться в качестве преобразующих элементов.
Различают однотактные, двухтактные (балансные), кольцевые преобразователи частоты, в которых используются один, два и более преобразовательных элемента с соответствующей фазировкой колебаний сигнала и гетеродина.
Конкретный тип преобразовательного элемента также находит отражение в наименовании преобразователя частоты: ПЧ на биполярном и полевом транзисторах, точечном диоде, туннельном и. обращенном диодах,
диоде с барьером Шотки, интегральной перемножительной микросхеме, микросборке и т. д.
Перечислим основные качественные показатели ПЧ:
коэффициент преобразования
К_а = U J Ос или KJ, — U J Ее, где Ес — ЭДС источника сигнала;
входное сопротивление (проводимость) ZBX =J/C//C,JKBX = l/Zexi
выходное сопротивление (проводимость) ZBblx - U „II
= 1/7
1' ВЫ X»
число и интенсивность побочных каналов приема, порождаемых преобразователем частоты.
В некоторых случаях существенны уровень собственных шумов ПЧ, уровень паразитного излучения гетеродина и влияние преобразователя частоты на электромагнитную совместимость приемного устройства с другой радиоаппаратурой комплекса.
Несмотря на разнообразие используемых преобразовательных элементов и нагрузочных систем, возможно построение единой теории для описания процессов, происходящих в любом преобразователе частоты. Она предполагает выполнение таких условий, как «малость» сигнала (Uc > Uг) и безынерционность преобразовательного элемента.
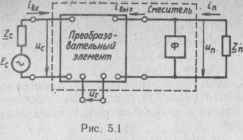
В общем случае преобразователь частоты можно представить в виде структурной схемы рис. 5. 1. К преобразовательному элементу приложены три напряжения — сигнала ис гетеродина иг и промежуточной частоты «„.
Фильтр Ф имеет прямоугольную частотную характеристику, причем в полосе прозрачности сопротивление этого фильтра для токов, частота которых лежит в зоне промежуточной частоты, равно бесконечности, а для токов других частот — нулю.
Для спектральных зон, близких к зоне частоты /„, фильтрация осуществляется нагрузкой преобразователя частоты Z„. В схеме рис. 5. 1 все фильтрующие функции вне зоны частоты f„ выполняет фильтр Ф.
Напряжение сигнала подается на вход преобразовательного элемента от источника сигнала с ЭДС и внутренним сопротивлением Zc (входной фильтр преобразователя частоты).
Преобразовательный элемент считается безынерционным. В этом случае входной и выходной токи в каждый момент времени определяются мгновенными значениями напряжений и,., «„, иг:

(5.
Обычно амплитуды напряжений ис, Uи малы по сравнению с амплитудой напряжения U г, т. е. выражение (5.1) можно разложить в двойной ряд Тейлора в точке, задаваемой мгновенными значениями напряжения иг, и учесть только первые (линейные) члены этого ряда. Для выходного тока получим выражение

(5.2)
где индексы «О» указывают, что соответствующие функции определяются в рабочей точке, задаваемой совместным действием постоянных напряжений питания и гетеродина. Обычно напряжение гетеродина является гармоническим колебанием:
иг = U\ cos со,, t, (5.3)
поэтому функции 0вых)о, (-^р)о.
I ,)о являются периодическими
и могут быть р-азложены в ряд Фурье. По своему смыслу функция S =
diuuxlduc есть некоторая прово; мость, которая может быгь назва обобщенной крутизной преобразу щего элемента, а функц <?''ных д"п diBblx/duabtx - G(— (обобщенной выходной npoeoduMocmi Эти параметры являются обобщ< ными, так как нагрузка может бь включена в цепь любого электрс преобразовательного элемента и i пряжение ис может также подавать на любой его электрод.
Выбрав начало отсчета так, что соответствующие функции были ч ными, можно записать:

Здесь /„, S0, Gi0 — постоянные i ставляющие выходного тока, к{ тизны и выходной проводимости; i S„, G,„ — амплитуды п-х гармон указанных величин.
Выделим из спектра сигнала од частотную составляющую:






